SP1815 WA - Problems Collection (Volume X)

## 题目背景 您需要解决十道数学题。

没有输入

输出一共有$10$行，第$i$行的数$result_i$表示第$i$个子任务的答案。

### 子任务1 定义一个函数$P(x)=x^5+a_1x^4+a_2x^3+a_3x^2+a_4x+a_5$。已知当$k$等于集合$\{1,2,3,4\}$中的任意一个元素时，有$P(k)=2007k$。求$P(10)-P(-5)$。 ### 子任务2 $100$个正整数$a_1,a_2,a_3 \dots a_{100}$的和为$2007$。求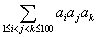的最大可能值。 ### 子任务3 计算$100101102103104 \dots 498499500$除以$126$的余数。 ### 子任务4 定义前$n$个几何级数的和$\{a_n\}s_n$。已知$s_7=7,s_{14}=2014$。求$s_7(s_{21}-s_{14})$。 ### 子任务5 如果一个正整数$k$满足$k≥4$且$k!$可以写成$k-3$个连续正整数的乘积，那么$k$在集合$S$内，否则$k$不在集合$S$内。求集合$S$内所有元素之和。 ### 子任务6 一个正方形的两个顶点正好在函数$y=2x-17$上，另外两个则在函数$y=x^2$上。求此正方形的两个不同的可能面积之和。 ### 子任务7 $A,B,C,D$是空间中的四个固定点，它们不在同一平面上。求在此空间内满足以下条件的平行六面体的数量：$A,B,C,D$都是此平行六面体的顶点。 ### 子任务8 多项式$x^2-x-1$整除多项式$a_1x^{17}+a_2x^{16}+1$求$a_1 a_2$。 ### 子任务9 $x$是锐角。求$(\sin x +\cos x) \div (\sin x +\tan x) + (\tan x +\cot x) \div (\cos x +\tan x) + (\sin x +\cos x) \div (\cos x +\cot x) + (\tan x +\cot x) \div (\sin x +\cot x)$的最小值。 ### 子任务10 $x,y,z$都是实数，$m,n$是正整数，已知$x^4+y^4+z^4=m \div n$，$xy+yz+xz=1$，$5(x+1 \div x)=12(y+1 \div y)=13(z+1 \div z)$，$m$和$n$的最大公约数是$1$（即$m$和$n$互质），求$m+n$。