SP21395 OHANIBTR - Ohani And Binary Search Tree

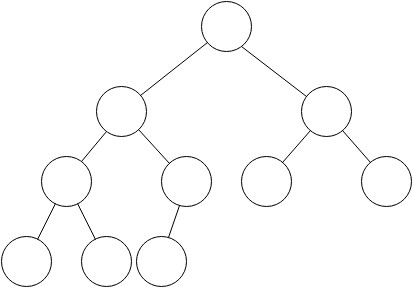
Ohani 最近学习了有关完全二叉树和二叉搜索树的知识。她希望创建一个同时具备完全二叉树结构和二叉搜索树性质的树，这种树称为完全二叉搜索树（CBST）。为了实现这一目标，Ohani 从一个排序好的数组中逐一取出数值，插入到一个完全二叉树中，从而构建出一棵符合要求的 CBST。 二叉搜索树的定义是：对于每个节点 $u$，$u$ 的值大于其左子树的所有节点值，并且小于其右子树的所有节点值。 完全二叉树的定义是：除最后一层外，其余各层节点数都达到最大，并且最后一层的节点尽量靠左，因此，对于 $n$ 个节点，有且仅有一种完全二叉树形态。下图展示了一个含有 10 个节点的完全二叉树。 

输入的第一行是一个整数 $T$，表示测试用例的数量（$1 \le T \le 5$）。 紧接着每个测试用例有两行数据。第一行包含一个整数 $N$，代表数组中元素的个数（$1 \le N \le 100000$）。 第二行是 $N$ 个互不相同的整数，每个整数都在 $1$ 到 $N$ 之间。

对于每个测试用例，输出三行。 - 第一行输出测试用例的编号。 - 第二行输出将数组排序所需的最少步数。 - 第三行输出从 $1$ 到 $N$ 的每个数在构建的 CBST 中对应的父节点。其中，根节点的父节点记为 $-1$。 例如，对于数组 `1 4 2 3`，CBST 的输出如下： ``` 2 3 -1 3 ``` 解释：节点 1 的父节点是 2，节点 2 的父节点是 3，节点 3 是根节点，因此其父节点为 -1，节点 4 的父节点是 3。

- 测试用例数 $1 \le T \le 5$ - 数组元素数 $1 \le N \le 100000$ **本翻译由 AI 自动生成**