SP21395 OHANIBTR - Ohani And Binary Search Tree

Ohani has recently learned about complete binary tree and binary search tree. Now she wants to create a complete binary tree and insert some value in the nodes such that it maintains the property of a binary search tree. She calls this tree Complete Binary Search Tree. So she takes a sorted array and one by one she inserts the values in a complete binary tree to create Complete Binary Search Tree (CBST). A binary tree is called a Binary Search Tree if for each node u, the value of u is greater than every value in the left subtree of u and is less than every value in right subtree of u. 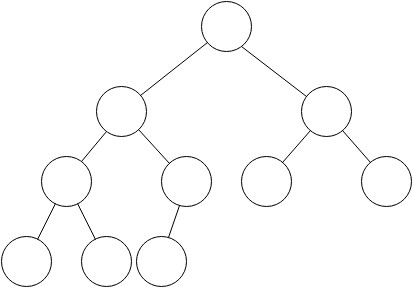A binary tree is said to be complete if all its levels, expect possibly the last, have the maximum number of possible nodes, and if all the nodes at the last level appears as far left as possible. So, there is a unique complete tree for n nodes. Here is a complete tree of 10 nodes. 

The first line of the input contains an integer T (1

For each test case, you need to output the case number on the first line. In the second line you have to output the minimum numbers of steps required to sort the array. In the third line, for each value from 1 to N, the parent of these values in the built CBST. The parent of the root is -1. For example, for if the given array is: 1 4 2 3, then the output for the CBST is, 2 3 -1 3 Because, the parent of value 1 is 2, the parent of value 2 is 3, 3 is the root, so, it's parent is -1, the parent of 4 is 3.