SP27213 PERIOD5 - Periodic function, trip 5

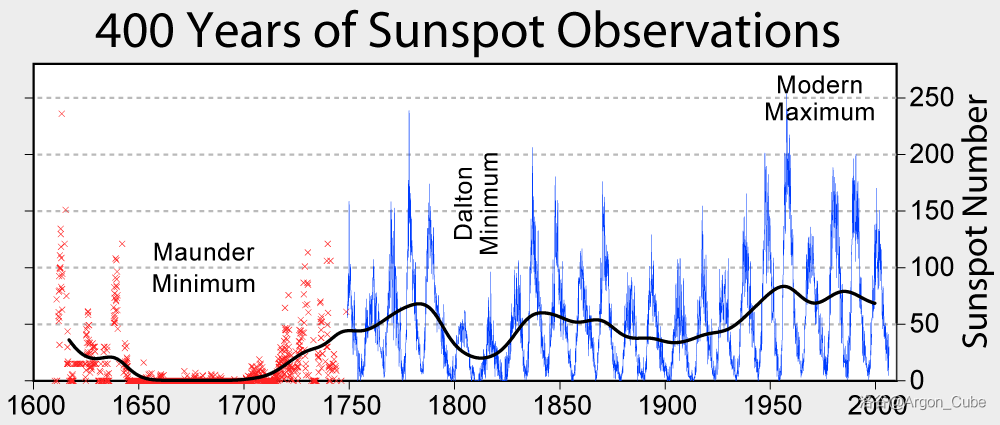
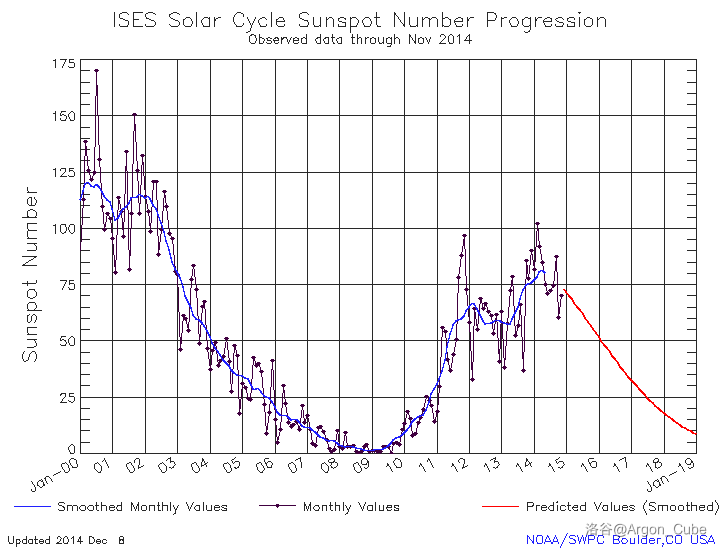
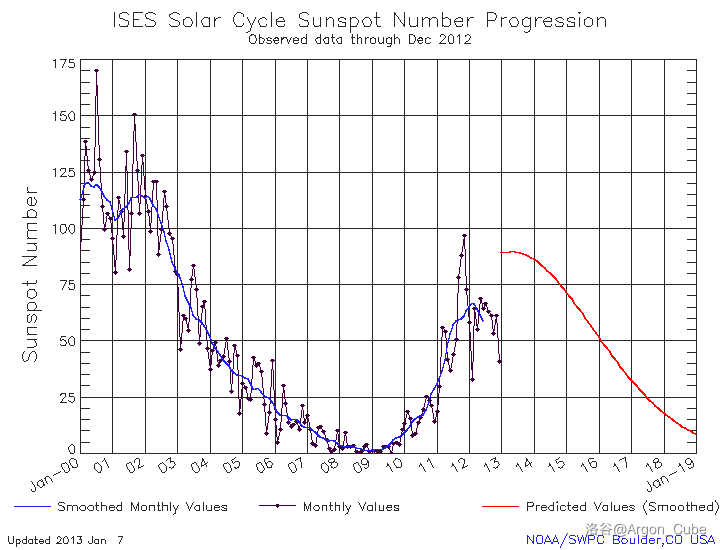
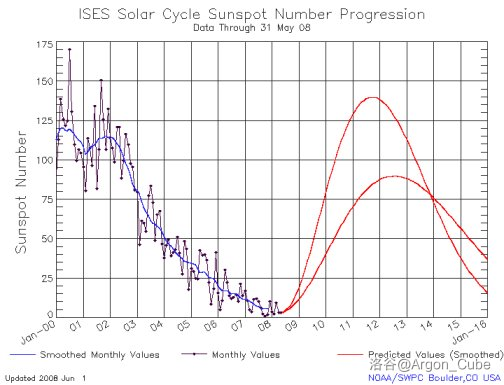
[太阳活动周期](http://en.wikipedia.org/wiki/Solar_cycle)的预测对多个机构和行业团体非常重要，因为它能直接影响低地球轨道卫星的寿命。这是由于卫星受到的空气阻力与太阳活动周期密切相关 \[...\]。[(NOAA)](http://www.swpc.noaa.gov/products/solar-cycle-progression)  太阳黑子数量统计表，数据分别为 2008 年 5 月、2012 年 12 月、2014 年 11 月观测：  考虑定义域为 $\mathbb Z$，值域为 $\mathbb R$ 的**周期函数**，记它们构成的集合为 $V$。显然由于任意两个这样的函数周期的比值都是有理数，因此对于任意 $f,g\in V$ 有 $f+g\in V$，于是 $V$ 是一个向量空间。 以下我们会采用一种简化记号：我们用括号括起函数值的循环节代表函数，其中第一个数代表 $f(0)$。比如，若 $f=[2,4,7]$，那么有 $f(-1)=7,f(0)=2,f(1)=4,f(2)=7$，同理接下来 $f$ 的函数值就是 $2,4,7,2,4,7,2,4,7,\cdots$。$f$ 对应的 Python 代码为： ```python def f(x): return [2, 4, 7][x%3] # (with Python notations) # 2,4,7,2,4,7,2,4,7,2,4,7,2,4,7, ... ``` 本题中，你需要尝试预测一些周期函数。我们会给定一些点值，你需要插值得出其它的点值。

本题为 [SP22271 PERIOD3 - Periodic function, trip 3](https://www.luogu.com.cn/problem/SP22271) 的加强版。 给定正整数 $N$ 以及一个函数 $f(x)$。$f$ 的构造方式是，在 $V$ 中任取一些周期不超过 $N$ 的函数，并将它们相加得到 $f(x)$。 给定 $f(0),f(1),f(2),\cdots,f(N^2-1)$ 这 $N^2$ 个点值，以及 $N^2$ 个询问 $x_1,x_2,\cdots,x_{N^2}$，你需要对于所有 $1\leq i\leq N^2$ 求出 $f(x_i)$。 可以证明，$f(x)$ 一定存在且唯一。

第一行一个整数 $N$。 第二行 $N^2$ 个整数，第 $i$ 个整数为 $f(i-1)$。 第三行 $N^2$ 个整数，第 $i$ 个整数为 $x_i$。

一行 $N^2$ 个整数，第 $i$ 个整数为 $f(x_i)$。

### 数据范围 * $1\leq N\leq 257$ * $|f(i)|< 10^9(0\leq i