SP3251 SLINK - Slink

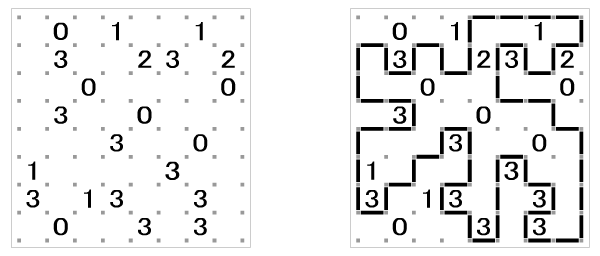
Slitherlink 是一种由日本公司 Nikoli 推出的谜题，该公司也因数独而闻名。Slitherlink 正在日益普及，相关书籍开始在全球范围内出现。这些谜题虽然容易理解，但解起来可能相当困难。谜题由一个点组成的矩形网格构成，每个单元格要么是空的，要么包含一个从 0 到 3 的整数。挑战在于连接这些点，形成一个环状路径（即每个顶点正好有两条边连接），使得每个填数字的单元格周围的边数与其中的数字相等。而没有数字的单元格可以有任意数量的连接边。有效的 Slitherlink 谜题总是设计得足够恰当，以确保独一无二的解法。下面是来自 Nikoli 网站的一个 Slitherlink 谜题及其解答示例。  东京大学的 Takayuki Yato 证明，一般的 Slitherlink 问题是 NP 完全的。（如果你不熟悉这一概念，简单来说，这意味着没有“高效”的算法能够解决这一问题。）然而，通过适当的修改和简单的启发式方法，我们可以编写程序来求解。我们新的谜题 Slink，只是在 Slitherlink 的基础上进行了一点改变，即不允许出现空单元格。即每个单元格都必须标明它所接触到的边的数量。下图展示了将 Slitherlink 转化为 Slink 的过程（新增的数字用灰色表示）。要注意，解法没有变化，只是给出的信息不同。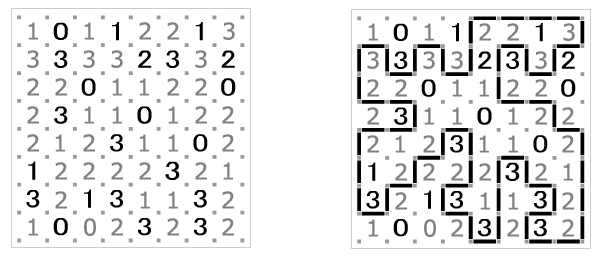  解决 Slink 的启发方法来自其自身的性质。例如，如果一个单元格内为数字 0，那么它周围不能有任何边，因此可以立刻将所有与 0 相邻的边排除在解路径之外。如果一个 3 与一个 0 相邻，所有与 0 相接的边被去除后，留下了 3 周围的三条边，而这些剩下的边因此必须包含在解路径中。下表具体描述了解决 Slink 谜题时应当应用的启发式规则。“x”表示不在解路径中的边，而线段表示是解路径的一部分。灰色部分是规则所依据的模式，黑色部分表示当匹配到某一规则时应该包括或排除的其他边。示例图片仅作示范用途，并非展示规则的所有可能情况。 ### 示例规则说明 1. 包含 0 的单元格周围没有边，因此所有边应从解路径中排除。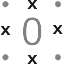  2. 如果一个单元格包含值 $n$，而剩下的 $n$ 条边尚未被排除，则这些剩余边必须包含在解路径中。  3. 如果一个单元格内已有 $n$ 条边属于路径，那么未包含在内的边即可排除。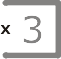  4. 相邻的两个 3 单元格，它们之间的边以及外边均是解路径的一部分。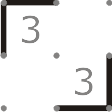  5. 如果两个 3 对角相邻，对应的对角线边必须在解路径中。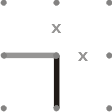  6. 如果某边进入一个顶点且只有一个出口，该出口��须在解路径中。  （规则继续） 请根据这些启发式规则仔细解题。

输入包含若干 Slink 谜题。每个谜题的第一行包含两个整数 $r$ 和 $c$，分别表示谜题的行数和列数。接下来 $r$ 行的数字表示每个单元格中的内容，从 0 到 3。保证每个输入有唯一的解。当输入行 $r$ 和 $c$ 都为 0 时，输入结束。

输出每个 Slink 谜题的解法，图形化表示。第一组数据编号为 1，第二组编号为 2，依次类推。输出时，用‘|’表示垂直边，用‘-’表示水平边，顶点交汇处用‘+’表示，数字两侧有空格。外围加上由‘#’组成的边框，每个谜题的左上角数字距边界右侧四个字符，距下方三个字符；右下角数字至左侧四个字符，上方三字符。 **本翻译由 AI 自动生成**