SP3912 MTREECOL - Color a tree

Bob 对“树”这种数据结构非常感兴趣。树是一个无向图，其中一个特殊的节点称为树根，并且从根到每个其他节点都有唯一的路径。 Bob 打算用笔对树的所有节点着色。一棵树有 $n$ 个节点，这些节点编号为 $1,2,\cdots,n$。假设一个节点着色需要 $1$ 个单位时间，并且不能同时对两个节点着色。另外，只有当父节点被着色时，才允许他对子节点着色。显然，在第一次着色中 Bob 只允许着色根。 每个节点都有一个“着色成本因子”$C_i$。每个节点的着色成本取决于 $C_i$ 和 Bob 完成该节点着色的时间。开始时，时间为 $0$。如果着色节点 $i$ 的完成时间是 $F_i$，则节点 $i$ 的着色代价是 $C_i\times F_i$。 例如，在图 $1$（下图）中示出了一个有五个节点的树。每个节点的着色成本因子分别为 $1,2,1,2,4$。Bob 可以以 $1,3,5,2,4$ 的顺序对树进行着色，最小总着色成本为 $33$。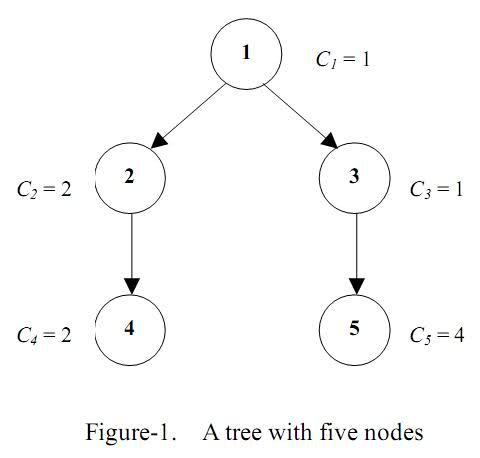  给定一个树和每个节点的着色代价因子，请帮助 Bob 找到着色所有节点的最小可能的总着色代价。

输入由多组测试数据组成。对于每组数据：第一行包含两个整数 $n$ 和 $r(1

对于每组测试数据，输出一行一个数，表示 Bob 所需的最小总着色代价，以对所有节点着色。 样例输出： ```markdown 33 ```