SP7192 INTEGMAX - Integral Maximization

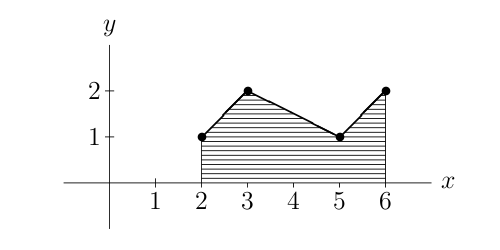
在 XY 平面上，有一组点的 x 坐标各不相同，这些点构成了一条多段线。我们通过对这些点按 x 坐标进行递增排序，并将各个点顺次相连来定义这条多段线。该多段线的积分即是在 x 轴和这条线之间的区域面积，范围从第一个 x 值到最后一个 x 值。举例来说，点集 {(5, 1), (3, 2), (6, 2), (2, 1)} 定义了一条多段线；这条多段线的积分值是阴影区域的面积，为 6。  给定 N 个不同的 x 值和 N 个 y 值，我们希望将它们配对生成平面上的 N 个点，使得这些点构成的多段线的积分尽可能大。

输入包含若干测试用例，每个测试用例由三行描述。第一行是一个整数 $N$，表示点的数量（$2 < N \leq 10^4$）。第二行由 $N$ 个不同的整数 $X_i$ 组成，数字之间用空格分隔，满足 $1 \leq X_i \leq 10^4$ 且 $X_i < X_{i+1}$（即升序）。第三行包含 $N$ 个整数 $Y_i$，同样以空格分隔，但没有特定顺序。输入的最后一行是一个单独的 -1，表示输入结束，这行不作为测试用例处理。

对于每个测试用例，输出一行，表示该测试用例中生成的多段线的最大积分，要求保留一位小数。注意，即使多段线的点的坐标是整数，其积分也总能被精确表示为一位小数。 **本翻译由 AI 自动生成**