SP8097 IOIISL08 - Islands

你准备游览一个公园，该公园由 $N$ 个岛屿组成，当地管理部门从每个岛屿 $i$ 出发向另外一个岛屿建了一座长度为 $L_i$ 的桥。桥是可以双向行走的。同时，每对岛屿之间都有一艘专用的往来两岛之间的渡船。但相对于乘船而言，你更喜欢步行。你希望经过的桥的总长度尽可能长，但受到以下的限制： - 你可以任意选择一个岛开始游览。 - 每一个岛都只能游览一次。 - 无论任何时间，你都可以从当前所在的岛 $S$ 去另一个从未到过的岛 $D$。从 $S$ 到 $D$ 有如下方法： - 步行：**仅当两个岛之间有桥时才可以步行**。如果你选择步行，桥的长度会累加到你步行的总距离中。 - 渡船：你可以选择这种方法，仅当没有**任何桥和以前使用过的渡船的组合**可以由 $S$ 走到 $D$。 注意，你不必游览所有的岛，也可能无法走完所有的桥。 请你编写一个程序，给定 $N$ 座桥以及它们的长度，按照上述的规则，计算你可以走过的桥的长度之和的最大值。

第一行包含一个整数 $N$，表示公园内岛屿的数目。 随后的 $N$ 行每一行用来表示一个岛。第 $i$ 行由两个以空格分隔的整数，表示由岛 $i$ 筑的桥。第一个整数表示桥另一端的岛，第二个整数表示该桥的长度 $L_i$。

一个整数，表示可能的最大步行距离。 ## 样例 ### 样例输入 ``` 7 3 8 7 2 4 2 1 4 1 9 3 4 2 3 ``` ### 样例输出 ``` 24 ```

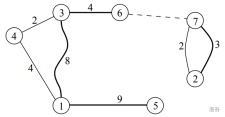
**样例解释**：  一共有 $7$ 座桥，如图所示。注意连接岛 $2$ 与岛 $7$ 之间有两座不同的桥。 其中一个可以取得最大的步行距离的方法如下： - 由岛 $5$ 开始。 - 步行长度为 $9$ 的桥到岛 $1$。 - 步行长度为 $8$ 的桥到岛 $3$。 - 步行长度为 $4$ 的桥到岛 $6$。 - 搭渡船由岛 $6$ 到岛 $7$。 - 步行长度为 $3$ 的桥到岛 $2$。 最后，你在岛 $2$，你的总步行距离为 $9+8+4+3=24$。 只有岛 $4$ 没有去。因为上述游览结束时，无法游览此岛。原因如下： - 你不可以步行去游览，因为没有桥连接岛 $2$ (你现在的岛) 与岛 $4$。 - 你不可以搭渡船去游览，因为你可由当前所在的岛 $2$ 到达岛 $4$。一个方法是：走 $(2-7)$ 桥，再搭你曾搭过的渡船由岛 $7$ 去岛 $6$，然后走 $(6-3)$ 桥，最后走 $(3-4)$ 桥。 对于 $100\%$ 的数据，$2\le N\le 10^6,1\le L_i\le 10^8$。