SP87 FOOTBALL - Football

Eric has a classic football that is made of $32$ pieces of leather: $12$ black pentagons and $20$ white hexagons. Each pentagon adjoins $5$ hexagons and each hexagon adjoins $3$ pentagons and $3$ hexagons. Eric drew a polygon (i.e. a closed line without intersections) along the edges of the pieces. The polygon divided the ball into two parts and Eric painted one of them green. 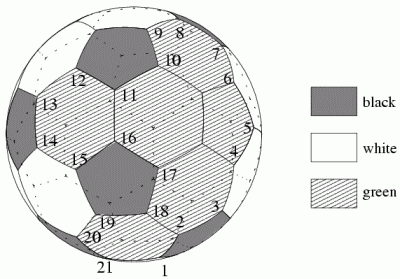 He is curious if given a description of the polygon you are able to compute the number of black, white and green pieces? ### Task Write a program that: - reads the description of a polygon, - computes the number of black, white and green pieces, - writes the result.

The input begins with the integer $t$, the number of test cases. Then $t$ test cases follow. For each test case, the first line of the input contains one integer n being the number of vertices of the polygon. The second line of the input contains n integers $a_{1}$ , $a_{2}$ ,..., $a_{n}$ separated by single spaces. Integer $a_{i}$ (equal $1$ or $2$) is the number of green pieces adjoining the $i$-th vertex of the polygon. The side of the polygon connecting the $n$-th and the first vertex always lies between two hexagons.

For each test case the first and only line of the output contains three integers $b$, $w$ and $g$ - the numbers of black, white and green pieces respectively.