T139092 盖斯
题目背景
盖斯定律定义:一个反应,在定压或定容条件下,不论是一步完成还是分几步完成,其反应热是相同的,总反应方程式的焓变等于各部分分步反应按一定系数比加和的焓变。(摘自百度百科)
题目描述
有一个 $n$ 个点的图,由 $m$ 条双向边连接着,如果一条双向边连接着 $u$ 和 $v$,从 $u$ 经过该条边到 $v$ 的边权为 $w$,那么从 $v$ 经过这条边到 $u$ 的边权就是 $-w$。
这个图满足以下条件:对于任意可以相互到达的两个点 $u$ 和 $v$,$u$ 到 $v$ 的**所有路径长度都相等**。
在这 $m$ 条边中,有一些边的边权给定,有一些边的边权不确定,你的任务是给这些边权不确定的边赋上一个边权,使得这个图满足上面所说的条件。
但是可能会出现无解的情况,所以可能需要舍弃一些边(即忽略一些边的影响)。
定义一个边集 $A$ 为舍弃集合当且仅当去掉边集 $A$ 以内的边后可以构造出满足条件的图。
定义舍弃集合 $A
输入格式
第一行两个数 $n,m$ 。
下面 $m$ 行,每行描述一条边,先输入一个整数 $op(op\in \{0,1\})$,如果 $op=0$,表示这条边边权确定,接下来输入三个整数 $u,v,w$,表示 $u$ 和 $v$ 之间连有一条双向边,其中从 $u$ 经过这条边走到 $v$ 的边权为 $w$;如果 $op=1$,表示这条边边权不确定,接下来输入两个整数 $u,v$,表示 $u$ 和 $v$ 之间连有双向边。
输出格式
输出第一行一个非负整数数 $tot$ ,表示你选出来的最小舍弃集合的大小。
接下来一行,输出共 $tot$ 个整数,从小到大输出你选出来的舍弃边集中的边的编号。
接下来一行,按输入顺序输出未给定边权的双向边从 $u$ 经过这条边走到 $v$ 的边权,请保证你输出的边权范围为 $[-2^{28},2^{28})$ 。
说明/提示
### 样例解释
样例一解释:
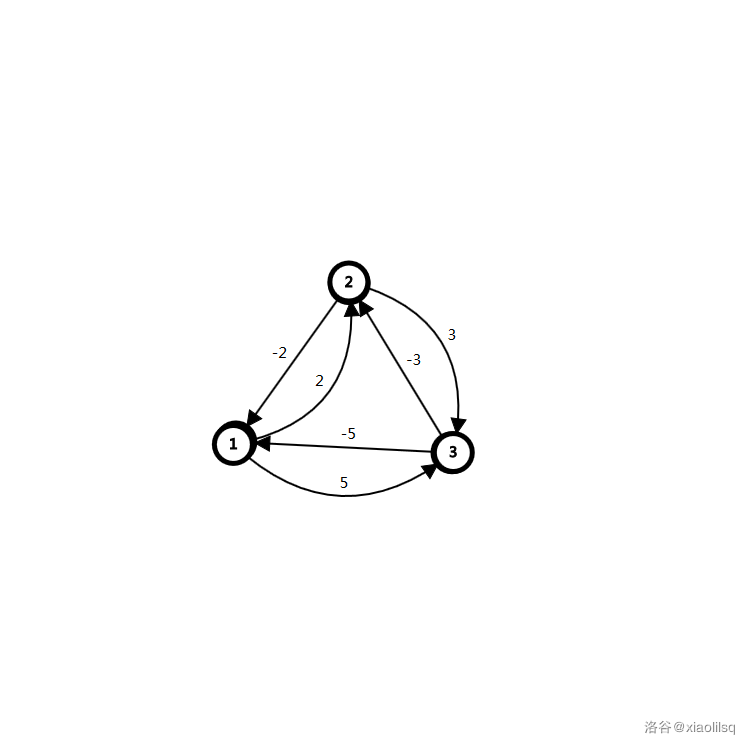
样例二解释:
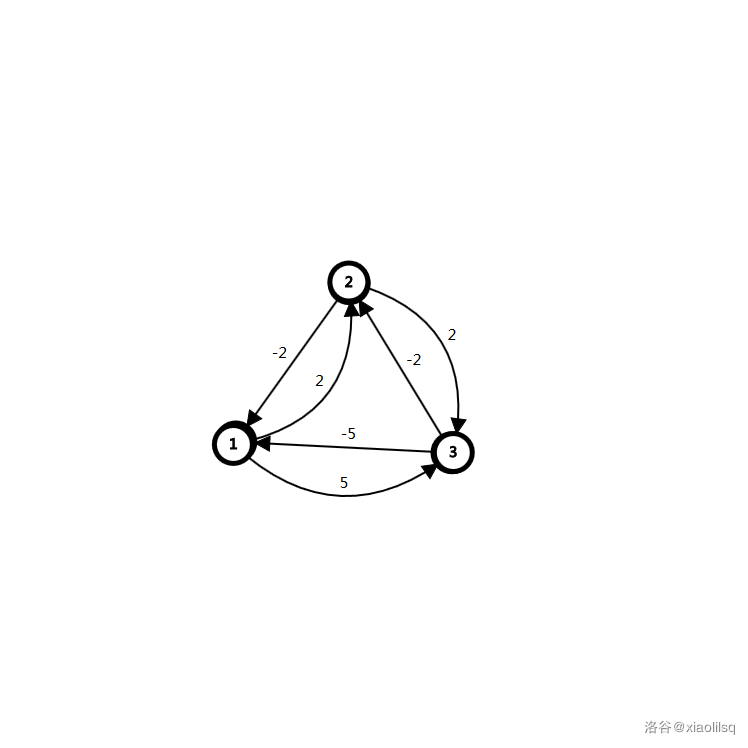
### 数据范围
对于 $100\%$ 的数据, $1\le n\le 2\times 10^5$,$1\le m\le 5\times 10^5$,$-300\le w\le 300$ 。
### 提示
请使用较快的输入输出。
请注意时间限制。