T148321 走廊巡逻

无

某学校某层的楼道是一个树形结构，有 $n$ 个交叉口、$n - 1$ 个走廊，每个走廊连接着两个交叉口，两两交叉口都可以互相到达，$n$ 个交叉口的编号分别 $1, 2, 3, ..., n$ ，**经过任意一条走廊的时间都是 $1$**，经过交叉口不需要花费时间。 每次自习课，学校会安排两个老师进行巡逻，每个教师会负责其中两个点之间的唯一简单路径，因此该教师会从 $0$ 时刻开始，在这条路径上来回走动。由于教师们拥有高超的眼力，因此不需要在观察上花费时间；并且由于教师们拥有充沛的精力，除非两个教师相遇在同一交叉口，教师们永远不会停下来。 如果两个教师相遇在同一个交叉口，由于周围没有教室和学生，他们会交流学生表现情况并立刻停止巡逻。 相遇：两个教师同一时刻在同一交叉口，**同一时刻在走廊不算相遇！！！** 若一个教师从 $0$ 时刻开始在 $u$ 到 $v$ 之间的简单路径上来回走动（若 $u = v$，则该教师在这个走廊点原地不动）$u, v$ 之间的唯一简单路径上的节点为 $u, d_1, d_2, ...,d_k, v$，则从 $0$ 到无穷时刻，每时刻该教师所在的交叉路口分别为 ： $$u, d_1, d_2, ...,d_{k-1}, d_k, v, d_k, d_{k-1}, ...,d_2,d_1,u,d_1,d_2,...d_k,v......$$ 如此循环往复无限走下去（可以看作一个 $u, d_1, d_2, ...,d_{k-1}, d_k, v, d_k, d_{k-1}, ...,d_2,d_1$ 的循环节）。 为了应对教师们的巡逻，学生们画出了这层的树形平面结构图，并且假想了 $m$ 种情况，对于每个情况他们想知道（这些问题是相互独立的）： * 若 $a$ 教师在 $u, v$ 的简单路径上来回走动，$b$ 教师在 $x, y$ 的简单路径上来回走动，那么他们第一次的相遇（在同一岔路口）时刻是什么时候（即停止巡逻的时刻）？如果两个教师永远无法相遇，请输出 $-1$。 学生们找到身为 Oier 的你，希望你借助计算机计算出结果。

第一行输入一个数 $n$，代表交叉口数量。 接下来 $n - 1$ 行，每行两个整数 $u, v$，代表交叉口 $u$ 和交叉口 $v$ 之间有一条走廊，经过时间为 $1$。 然后一行一个整数 $m$，表示假想的情况，即询问个数。 然后 $m$ 行，包含四个整数 $u, v, x, y$，即 $a$ 教师在 $u, v$ 的简单路径上来回走动，$b$ 教师在 $x, y$ 的简单路径上来回走动。

输出共 $m$ 行，第 $i$ 行表示第 $i$ 次的假想状况对应的答案，即两个教师第一次的相遇在同一岔路口的时刻，如果两个教师永远无法相遇，请输出 $-1$。

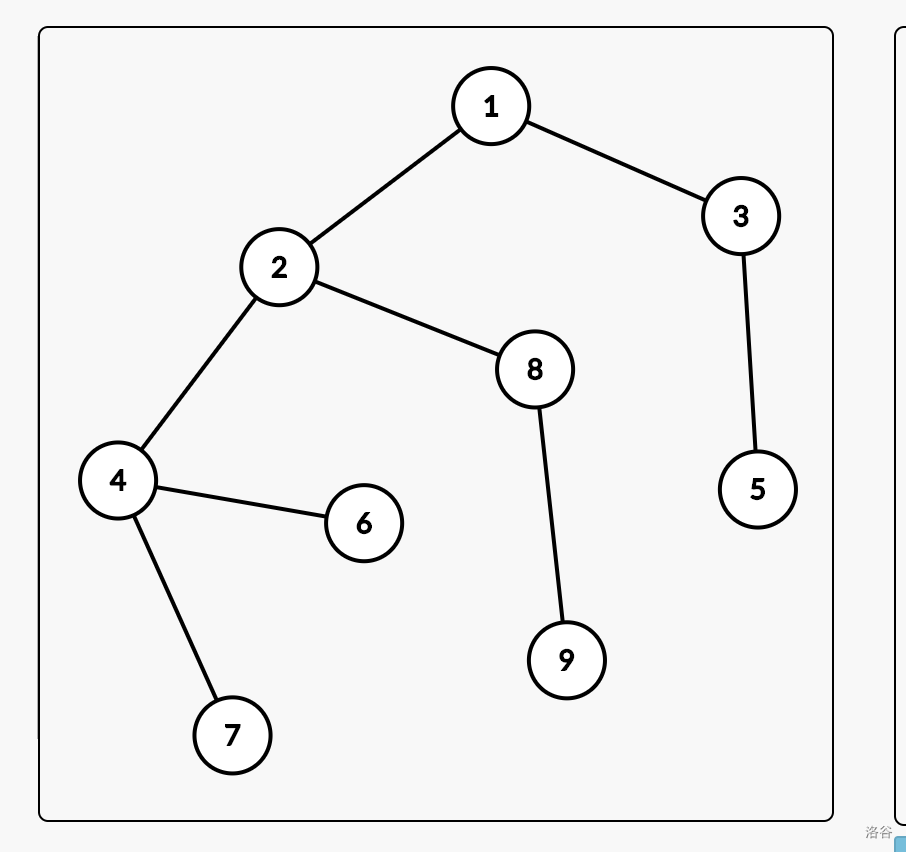
样例 #1 解释  如图。 第一个询问，$a$ 教师从 $0$ 时刻开始经过的点分别是 $6, 4, 2, 1, 2, 4, 6,...$，$b$ 教师经过的点是 $8, 2, 4, 7, 4, 2, 8,......$，两人会在 $2$ 到 $4$ 的走廊相遇，但永远不会再交叉口相遇，所以答案是 $-1$。 第二个询问，$1$ 时刻两人会相遇在 $4$ 号节点。 第三个询问，两个人一直都在 $4$ 号点 $0$。 第四个询问，两个人走的是两个互不相交的路径，因此答案是 $-1$。 第五个询问，两人会在 $6$ 时刻相遇于点 $2$。 对于 $100\%$ 的数据，满足 $1 \le n,q \le 2 \times 10^5$， $a, b, u, v, x, y$ 都是 $1$ 到 $n$ 之间的整数 子任务|所占分数|测试点编号|$n \le$ | $q \le$ | 特殊性质 -|-|-|-|-|- $1$|$10$|$1 \text{ ∼ } 2$|$100$|$100$|无 $2$|$10$|$3 \text{ ∼ } 4$|$2 \times 10^5$|$2 \times 10^5$| 所有情况都有 $x = y$ $3$|$10$|$5 \text{ ∼ } 6$|$2 \times 10^5$|$2 \times 10^5$| 所有情况都有 $u = y$ 且 $v = x$ $4$|$20$|$7 \text{ ∼ } 10$|$2000$|$2000$|无 $5$|$20$|$11 \text{ ∼ } 14$|$2 \times 10^5$|$2 \times 10^5$| 树退化成一条链，其中 $1$ 与 $2$ 有边，$2$ 与 $3$ 有边，......，$n - 1$ 与 $n$ 有边。 $6$|$30$|$15 \text{ ∼ } 20$|$2 \times 10^5$|$2 \times 10^5$| 无 **本题输入量较大，建议使用较快的输入方式**