T169751 Nephren

$$ \begin{aligned} &\Large\text{\color{black}終 \color{MediumOrchid}末 な に \color{DarkBlue}し \color{MidnightBlue}て}　\\ &\Large\text{\color{black}ま \color{MediumPurple}す か\color{MediumOrchid}？}\\ \quad\\ &\Large\text{\color{indigo}も \color{MediumOrchid}う 一 度 だ \color{MidnightBlue}け 、}\\ &\Large\text{\color{black}会 \color{purple}え ま す \color{darkSlateBlue}か \color{black}？}\\ &\color{GoldEnrod}\tiny\text{Do\ \ you\ \ have\ \ what\ \ THE\ \ END?}\\ &\color{GoldEnrod}\tiny\text{May\ \ I\ \ meet\ \ you}\\ &\color{GoldEnrod}\tiny\text{once\ \ again?} \end{aligned}\\ \quad\\ \text{- Nephren -}\\ \quad$$ 为了不让悬浮大陆群毁灭，奈芙莲一直观测着这个末日的箱庭。 自己恐怕撑不了多久了。 奈芙莲现在有这样的自觉。 只要身为观测者的奈芙莲在这里，故事中的世界就可以继续存在。相反地，她一旦停止观测，整个世界就会和所有的故事一起放弃其存在。 她站在道路中央。 她站在黑暗之中。 场景一转，她置身于光芒之中。 景色又是一变，她来到了一片战场——

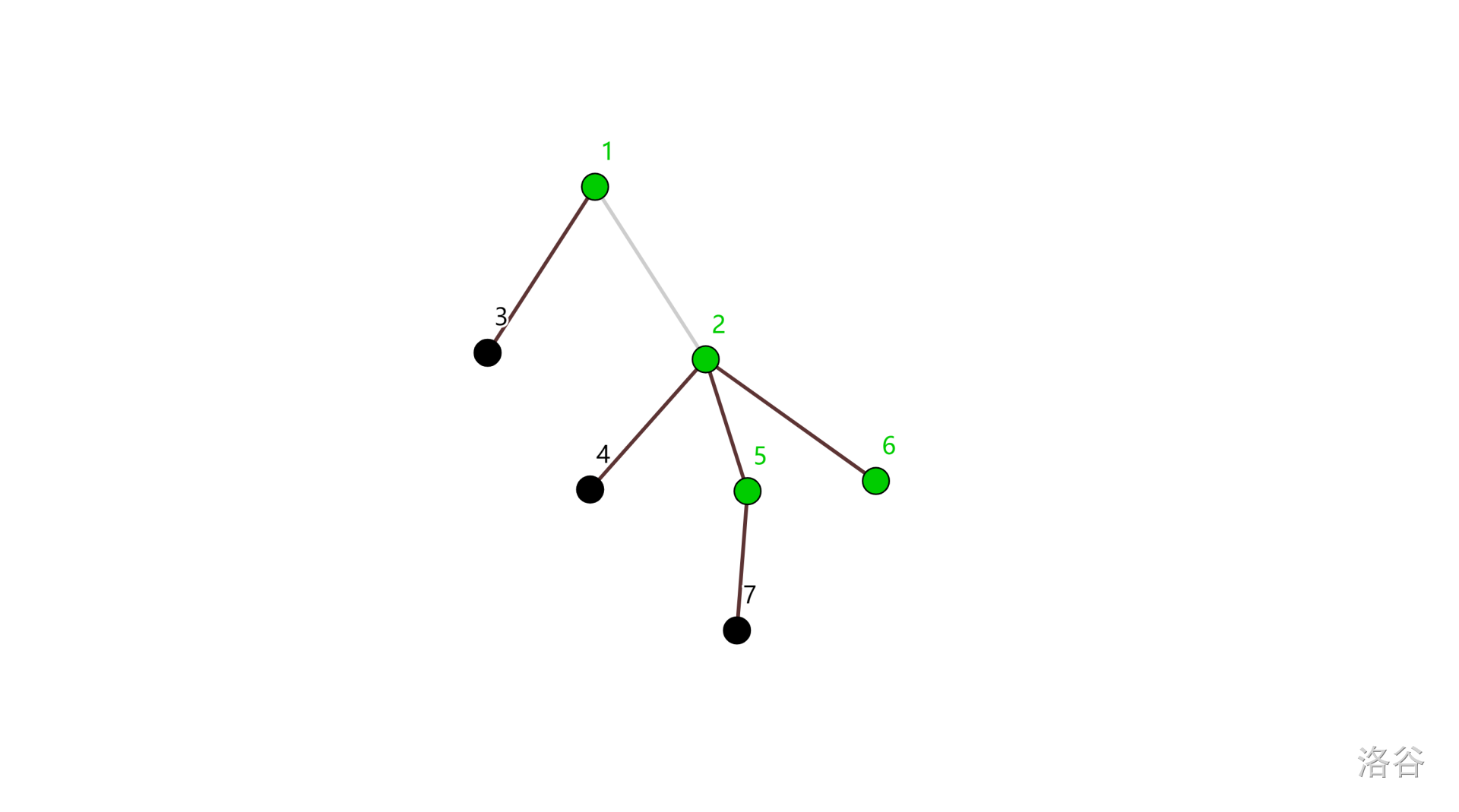
艾尔毕斯的余党——或者伪装成如此的什么东西——向护翼军的基地发起了入侵。 护翼军的基地可以看做一棵树 $T$，分为 $n$ 个节点，由 $n-1$ 条道路连通。 护翼军迅速响应，组织军队互相支援防守关键节点。 但敌人的潜入技术十分强大，所以他们可以从任何一条路中间出现并切断那条道路，让护翼军的基地分隔，这样子只有仍旧连通的节点可以互相支援。下面将连通的节点组成的一个极大连通子图记为 $A=(V_A,E_A)$。 在一个极大连通子图内，**几个连通（指可以只经过关键节点互达）的关键节点可以形成一个防守区块**。一个在 $A$ 中的极大防守区块能获得 $A$ 中所有节点的支援，因此**其战斗力为 $|V_A|$**。 基地的战斗力为各极大防守区块的战斗力之和。  上图是一种可能的基地情况，其中灰边是被敌人切断的边，绿点为关键节点。在上图中，$\{2,5,6\}$ 是一个极大防守区块，它在极大连通子图 $\{2,4,5,6,7\}$ 中，因此其战斗力为 $5$。而 $\{1,2,5,6\}$ 不是防守区块，因为它并不能通过未被切断的边连通。这种情况下基地的战斗力为 $7$。 奈芙莲并不知道基地的关键节点有哪些，所以她认为**每个节点都等概率地成为或不成为关键节点**。 奈芙莲也不知道敌人会采取什么方案入侵，所以她认为**每条边都等概率地会被切断或不切断**。 奈芙莲想知道在这种情况下，**基地战斗力的期望 $\bmod\; 998244353$**。 奈芙莲仍需要持续观测整片大陆，没有办法分心去计算，所以她把这个任务交给了你。奈芙莲眼前的光景转瞬即逝，所以她希望你在 1s 内告诉她答案。 如果你能够帮助她解决这个问题，她就能有一点动力撑到威廉回来。

第一行一个正整数 $n$。 第二行至第 $n$ 行每行两个正整数 $u,v$，表示节点 $u,v$ 之间有一条边连接。

一行一个非负整数，表示基地战斗力期望 $\bmod \; 998244353$。

### 样例解释 #### 样例 1 共有 $2^5$ 种情况，枚举可得战斗力期望为 $\dfrac{17}{8}$。 **[点此查看完整解释](https://www.luogu.com.cn/paste/l8qaw87h)** #### 样例 2 战斗力期望为 $\dfrac{205}{32}$。 ### 提示 本题读入量较大，**推荐使用较快的读入方式。** 对于分数 $\frac{a}{b}$ 取模 $P$ 表示寻找一个数 $m$ 使得 $bm\equiv 1\pmod{P}$，则 $\frac{a}{b}\equiv am\pmod P$。可以证明当 $P$ 为质数，$b\not\equiv 0 \pmod P$ 时答案存在且唯一。 ### 数据范围与约定 **本题使用 Subtask 捆绑评测。** 对于 $100\%$ 的数据，$n\le 10^6$。数据保证图连通。 | Subtask 编号 | 特殊性质 | 分数 | | :----------: | :----------: | :----------: | | 1 | $n\le10$ | $7$ | | 2 | $n\le20$ | $8$ | | 3 | $n\le100$ | $8$ | | 4 | $n\le1000,\forall(u,v)\in E,v=u+1$，即图的形态是一条链 | $12$ | | 5 | $n\le1000$ | $14$ | | 6 | $n\le10^5$| $17$ | | 7 | $\forall(u,v)\in E,v=u+1$，即图的形态是一条链 | $13$ | | 8 | 无 | $21$ |