T221406 办聚会 Choosing Cities

在 EF 国，有 $n$ 个城市，城市之间有 $n-1$ 条道路，**保证城市之间能互相到达**。第 $i$ 条道路连接城市 $u_i$ 和 $v_i$，长度为 $w_i$。 情人节要到了，有 $q$ 组人 win 想要团聚，共同庆祝情人节。第 $c$ 组人 win 共有 $k_c$ 个人，第 $j$ 个人在城市 $pos_j$。 公平起见，他们决定选择一个城市 $y$，使所有人到那个城市的距离相等。他们想知道共有多少个这样的城市，但是由于他们忙着贴贴，没时间思考这个问题，就只好请教你啦。

第一行两个整数 $n,q$。 接下来 $n-1$ 行，每行三个整数 $u_i,v_i,w_i$。 接下来 $q$ 行，首先输入一个整数 $k_i$，接下来输入 $k_i$ 个整数，第 $j$ 个整数为 $pos_j$。

$q$ 行，每行一个整数表示答案。

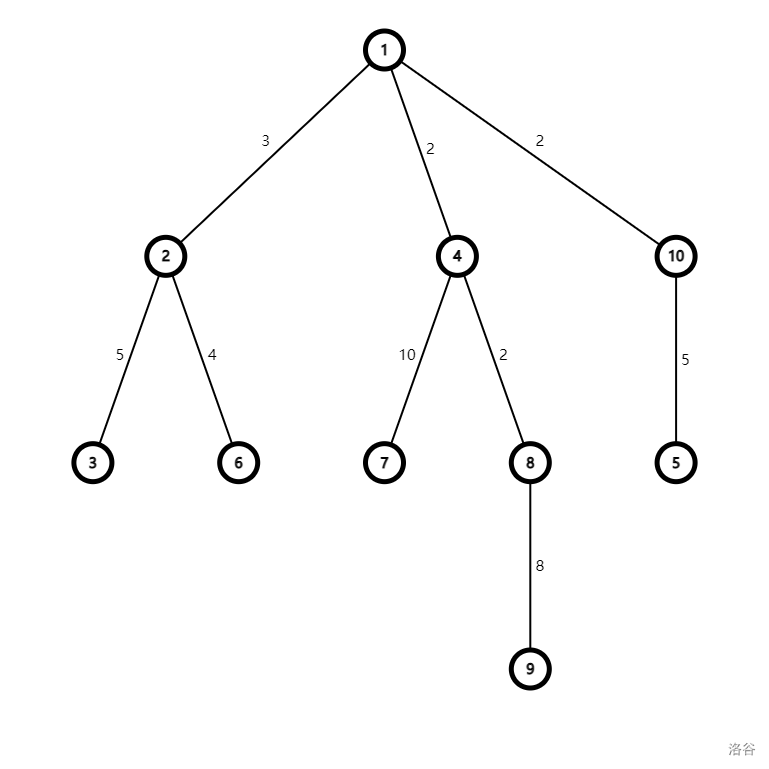
**【样例 1 解释】**  对于前两组人 win，他们可以选择在 $2$ 号和 $6$ 号城市团聚； 对于第三组人 win，他们可以选择在 $1$ 号、$2$ 号、$3$ 号、$4$ 号、$5$ 号、$6$ 号和 $10$ 号城市团聚； 对于第四组人 win，无论选择哪一个城市都无法使所有人到那个城市的距离相同； 对于第五组人 win，他们可以选择在 $4$ 号、$8$ 号和 $9$ 号城市团聚。 **【数据范围】** **本题采取捆绑测试。** | 子任务编号 | 分值 | 特殊性质 | | :----------: | :----------: | :----------: | | $1$ | $20$ | $n\le 100$，$q\le 10^4$ | | $2$ | $80$ | 无 | 对于 $100\%$ 的数据，$1\le n,\sum\limits_{i=1}^q k_i \le 10^6$，$1 \le u_i,v_i\le n$，$1\le q \le 2\cdot10^5$，$1\le w_i\le 10^4$。