T256110 [CZOI Online #2] 南瓜
题目描述
一天明陌来到 Caiwen 家做客,Caiwen 决定拿出自己最喜欢的南瓜来招待明陌。
Caiwen 对南瓜有自己独到的见解,他最喜欢圆形的南瓜。 我们规定一个南瓜圆的程度为**圆度**。
对于所有的南瓜,Caiwen都测量出其高度 $h$ 和宽度 $d$ 。我们可以粗略地认为 $\frac{h}{d}$ 的数值越接近于 $1$ 的南瓜越接近圆形,即圆度越大,特别规定此时的圆度为 $\frac{h}{d}$ 与 $1$ 的差值。
但 Caiwen 只能对单个的南瓜采用这种方式评估其圆度,对于若干个南瓜,Caiwen 需要计算出这堆南瓜的**平均圆度**,公式如下:
$$\frac{\sum h_i}{\sum d_i}$$
平均圆度即可视为这堆南瓜的圆度。
由于 Caiwen 非常珍惜他的南瓜,所以他只会拿出 $k$ 个南瓜来招待明陌,且这 $k$ 个南瓜的圆度最大。
现在你需要帮助 Caiwen 计算出用来招待明陌的南瓜的圆度是多少。
输入格式
第一行:两个数 $n$ 和 $k$,表示 Caiwen 决定在自己拥有的 $n$ 的南瓜中选出 $k$ 的南瓜招待明陌。
第二行 $n$ 个数,第 $i$ 个数表示第 $i$ 个南瓜的高度 $hi$。
第三行 $n$ 个数,第 $i$ 个数表示第 $i$ 个南瓜的宽度 $di$。
输出格式
一行,一个实数,Caiwen 挑选出用来招待明陌的南瓜的平均圆度,精确到小数点后4位。
说明/提示
**样例#1解释**
选择第 $2$、$3$、$4$ 个南瓜,平均圆度为 $\frac{2+4+1}{3+9+3}$。可以证明这是最优方案。
**样例#2解释**
第 $1$ 个南瓜的 $\frac{h}{d}$ 值与 $1$ 最接近。
**数据规模及约定**
对于 $100\%$ 的数据:$1≤k≤n≤10^6$,$1≤h_i≤d_i≤10^6$。
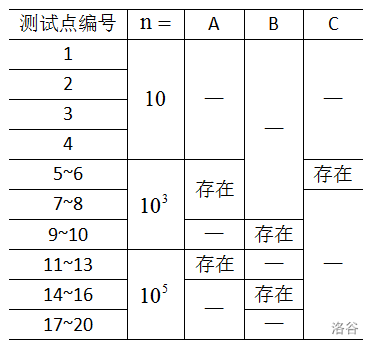
A、B、C 为特殊性质。
A:保证 $k=1$。
B:保证 $k=n$。
C:保证所有的 $d_i$ 相同。