T297881 [CZOI Online #2] 黑盒(part)
题目背景
本题完整版:
https://hydro.ac/d/czoi2023/p/P1 (前16个测试点)
https://hydro.ac/d/czoi2023/p/P2 (后4个测试点)
题目描述
Caiwen 和明陌发现了三个黑盒,于是对三个黑盒进行了研究。
Caiwen 研究首先观察了第一个黑盒,发现这个黑盒中有**无穷多个**数,这可把 Caiwen 吓了一跳,但 Caiwen又仔细研究了一下,发现这个黑盒中的数是有规律的,他是 $n$ 个数不断重复形成的。
明陌则研究第二个黑盒,发现这个黑盒里什么都没有,于是继续研究第三个黑盒。他发现,向第三个黑盒中放入数字后,第三个黑盒会将放入的数字首尾拼接,形成一个非常大的数字。
Caiwen 对这三个黑盒很感兴趣,于是和明陌玩起了一个游戏,Caiwen 给明陌的操作有四种,具体如下:
1. 将第一个黑盒中的第一个数放到第二个黑盒中。
2. 将第二个黑盒中**最早**被放入的数放入第三个黑盒中。
3. 将第二个黑盒中**最晚**被放入的数放入第三个黑盒中。
4. 输出第三个黑盒中最后形成的数,然后将第三个黑盒清空。
Caiwen 一下子给了明陌 $q$ 个操作,明陌一时招架不住,于是请你来帮忙解决这个问题。
输入格式
第一行,一个数 $n$ 。
第二行, $n$ 个数,表示第一个黑盒中不断重复的数。
第三行,一个数 $q$ ,表示操作数目。
第四行,一个仅包含数字 $1$、$2$、$3$、$4$ 的字符串,表示操作的类型。
输出格式
对于每个 $4$ 操作,你需要输出第三个黑盒中形成的数。特别地,如果第三个黑盒中没有数,你仍需要输出 $0$ 。
说明/提示
**样例#1解释**
这 $6$ 个操作分别为:
1. 把 `1` 放入到了黑盒 $2$ 中。
2. 把 `1` 放入到了黑盒 $2$ 中。
3. 把 `4` 放入到了黑盒 $2$ 中。
4. 因为第一个 `1` 是三个数中最早被放入黑盒 $2$ 中的,所以 `1` 被放入到了黑盒 $3$ 中。
5. 因为第一个 `4` 是两个数中最晚被放入黑盒 $2$ 中的,所以 `4` 被放入到了黑盒 $3$ 中。
6. 黑盒 $3$ 中的数字 `1`、`4` 被依次连接在了一起,形成一个大数 `14`。
**样例#2解释**
这 $15$ 个操作分别为:
1. 把 `11` 放入到了黑盒 $2$ 中。
2. 把 `22` 放入到了黑盒 $2$ 中。
3. 把 `0` 放入到了黑盒 $2$ 中。
4. 把 `11` 放入到了黑盒 $2$ 中。
5. 把 `22` 放入到了黑盒 $2$ 中。
6. 因为第一个 `11` 是五个数中最早被放入黑盒 $2$ 中的,所以 `11` 被放入到了黑盒 $3$ 中。
7. 因为第二个 `22` 是四个数中最晚被放入黑盒 $2$ 中的,所以 `22` 被放入到了黑盒 $3$ 中。
8. 因为第二个 `11` 是三个数中最晚被放入黑盒 $2$ 中的,所以 `11` 被放入到了黑盒 $3$ 中。
9. 因为第一个 `22` 是两个数中最早被放入黑盒 $2$ 中的,所以 `22` 被放入到了黑盒 $3$ 中。
10. 黑盒 $3$ 中的数字 `11`、`22`、`11`、`22` 被依次连接在了一起,形成一个大数 `11221122`。
11. 黑盒 $3$ 中已经没有了数字,输出 `0`。
12. 把 `0` 放入到了黑盒 $2$ 中。
13. 因为第一个 `0` 是两个数中最早被放入黑盒 $2$ 中的,所以 `0` 被放入到了黑盒 $3$ 中。
14. 因为第二个 `0` 是一个数中最晚被放入黑盒 $2$ 中的,所以 `0` 被放入到了黑盒 $3$ 中。
15. 黑盒 $3$ 中的数字 `0`、`0` 被依次连接在了一起,形成一个大数 `0`。
**数据规模及约定**
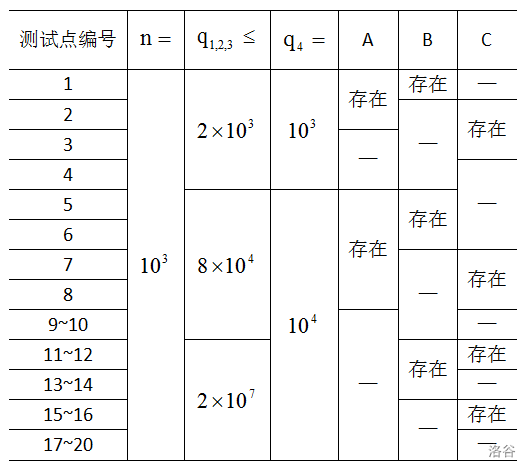
A、B、C 为特殊性质,$q_{1,2,3}$ 表示操作 $1$、$2$、$3$ 次数之和。$q_4$ 表示操作 $4$ 的次数。
对于所有数据,保证操作 $2$ 和 $3$ 执行时,第二个黑盒中一定有数;所有操作结束后,第二个和第三个黑盒中没有数;所有的数均在 `int` 范围内。
A:保证第一个黑盒中不存在数字 $0$ 。
B:保证只有操作 $2$。
C:保证只有操作 $3$。