T304485 [CZOI2023] 到达
题目描述
现在给你一个 $n$ 个点,$m$ 条边的无向图,并给出 $q$ 个询问,每次询问给出一个点 $a$ 和一个数 $L$,你需要回答能不能从点 $1$ 出发,恰好经过 $L$ 条边到达点 $a$,**边可以重复走**。
输入格式
第一行,三个数 $n,m,q$。
接下来 $m$ 行,每行两个数 $u,v$,表示存在一条连接 $u$ 和 $v$ 的无向边。
接下来 $q$ 行,每行两个数 $a,L$,表示一个询问。
输出格式
共 $q$ 行。如果可以从点 $1$ 出发,恰好经过 $L$ 条边到达点 $a$,那么你输出 `Yes`,反之你输出 `No`。
说明/提示
**样例#1解释**
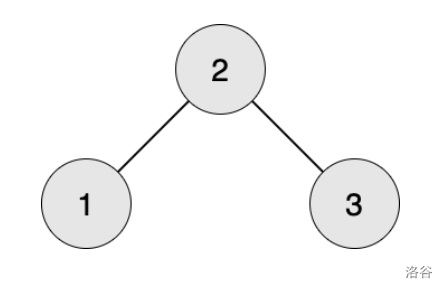
1. 点 $1$ 不可以经过恰好 $1$ 条边到达点 $1$。
2. 点 $1$ 可以经过恰好 $1$ 条边到达点 $2$。
3. 点 $1$ 不可以经过恰好 $1$ 条边到达点 $3$。
4. 点 $1$ 可以先到达点 $2$,再从点 $2$ 回到点 $1$,恰好经过 $2$ 条边。
5. 点 $1$ 不可以经过恰好 $2$ 条边到达点 $2$。
6. 点 $1$ 可以直接经过 $2$ 条边到达点 $3$。
**样例#2解释**
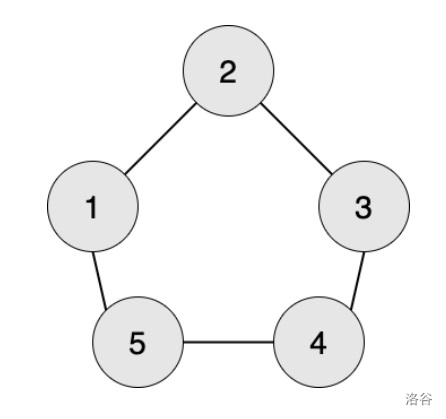
1. 点 $1$ 不可以经过恰好 $1$ 条边到达点 $1$。
2. 点 $1$ 可以先到达点 $2$,再回到点 $1$ ,恰好经过 $2$ 条边。
3. 点 $1$ 不可以经过恰好 $3$ 条边到达点 $1$。
4. 点 $1$ 可以按 `1->2->3->2->1` 的方式到达点 $1$ ,恰好经过 $4$ 条边。
5. 点 $1$ 可以按 `1->2->3->4->5->1` 的方式到达点 $1$ ,恰好经过 $5$ 条边。
**数据规模及约定**
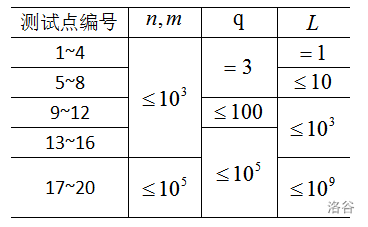
对于 $100\%$ 的数据,$1\le u,v,a\le n$。