T320926 [DSOI Round #1]相控阵

三个小时后，月球将突破地月洛希极限，地球将会变成一片火海，人类的文明将会在三天内断绝…… 可是，勇敢的人类从未屈服，他们决定在月球上放置地球上所有的核弹。 人类的内斗从未停歇，即使在此时，核弹的密码还没有完全公布，破译密码的进程缓慢，只好使用相控阵来放置核弹。

现在有 $ n $ 颗核弹密码已被破译，我们把每 $ 5 $ 枚核弹组合到一起，$ 5 $ 枚核弹（$ 1 \sim 5,6 \sim 10,11\sim 15 ...... $）中，第一枚和第二枚，第二枚和第三枚……第五枚和第一枚之间存在潜在反应关系，可能会产生一定的强力反应。**核弹有两种模式**，只有两颗核弹处于 **不同模式** 下，核弹的潜在反应关系才会生效，产生强力反应。$ a_i $ 表示第 $ i $ 枚核弹和 $ i+1 $ 枚的潜在反应关系强度，即产生强力反应的效果。（ 特殊的，当 $ i $ 为 $ 5 $ 的倍数即为第 $ i $ 枚和第 $ i-4 $ 枚核弹产生强力反应的效果）。 相控阵对月球产生的作用力即为强力反应效果之和。你需要求出有多少种模式开启方案，使得两种模式的核弹数量相等，且总作用力最大，输出方案数模 $ 998244853 $ 的结果。 即使需要取模，也是人类最后的希望，请你……一定要在 1s 内求出结果啊。

第一行一个整数 $n$， 代表核弹密码的总数 接下来 $ n $ 个正整数 $ a_i $，表示每条核弹密码产生的强力反应。 数据保证 $ n $ 是 $ 10 $ 的倍数。

一行一个整数，表示答案对 $998244853$ 取模的值。

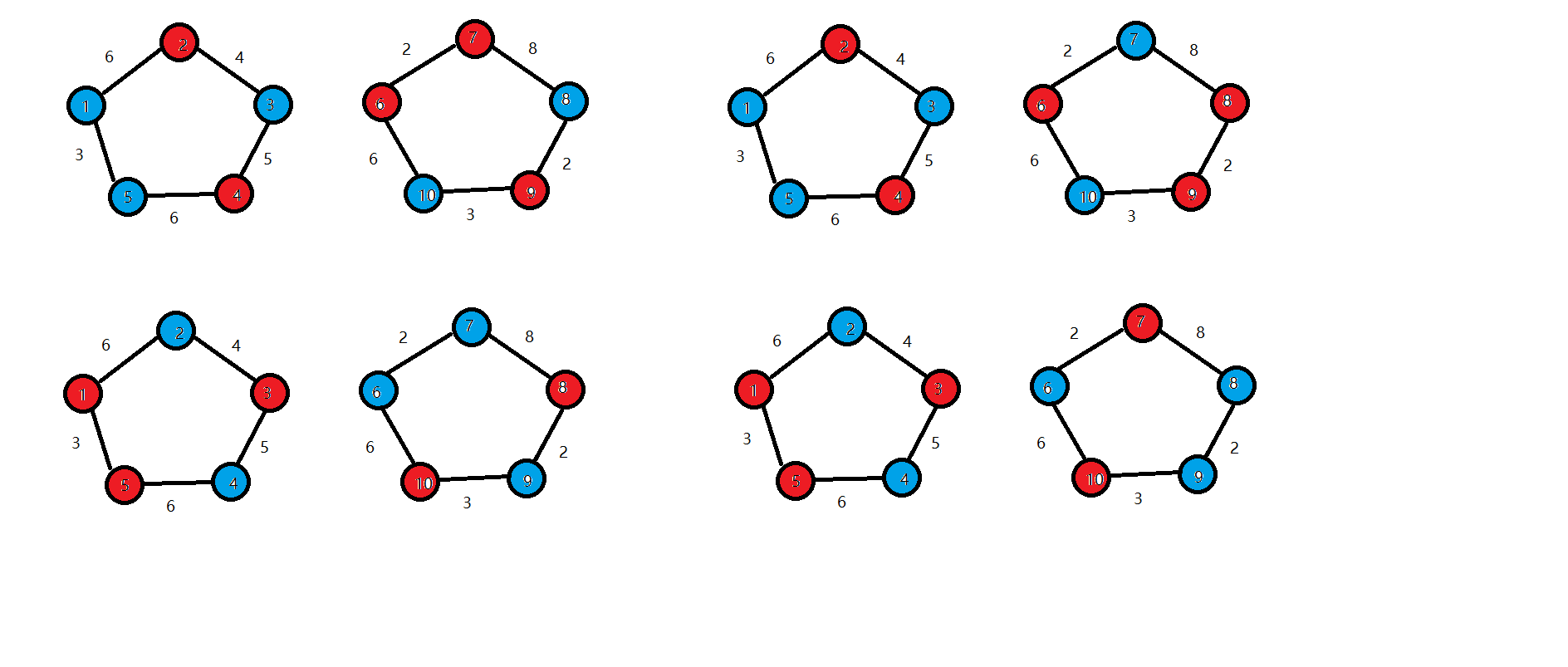
### 【样例解释】 样例1如图所示  红色和蓝色分别为核弹的不同模式。 易求最大值为 $40$。 共有四种方案。 ### 【数据约定】 对于 $ 20\% $ 的数据，满足 $ n \le 20 $。 对于 $ 40\% $ 的数据，满足 $ n \le 100 $。 对于 $ 60\% $ 的数据，满足 $ n \le 5000 $。 对于全部数据，保证 $10\leq n\leq 3 \times 10^5$，$1 \leq a_i \leq 10^3$，并保证 $n$ 是 $10$ 的倍数。 逆元： $\frac{a}{b} \bmod m=a \times b^{-1} \bmod m$ 其中 $m$ 为一个质数 定义 $b^{-1}$ 为 $b$ 在模 $m$ 意义下的逆元 则 $b^{-1}\times b \bmod m=1$ 费马小定理： $a^{m-1} \equiv 1 \bmod m \iff a\times a^{m-2} \equiv 1 \bmod m$ 即 $a$ 在模 $m$ 意义下的逆元为 $a^{m-2}$ 提示：请仔细读题