T417336 跳房子

跳房子，也叫跳飞机，是一种世界性的儿童游戏，也是中国民间传统的体育游戏之一，趣味性、娱乐性极强，曾深受广大儿童的喜爱。

现在我们给出一种简易跳房子游戏的玩法： $n$ 个格子从左到右一字形排开，从左到右依次被标号为 $1, 2, \cdots, n$。每一个格子上都有一个正整数，$i$ 号格子上的正整数是 $a _ i$。 这个游戏的规则如下：初始时玩家站在 $1$ 号格子上，需要做若干次跳跃。每一次跳跃时，玩家需要从当前格子向前跳「当前格子上写的整数」数量的格子。形式化地讲，如果玩家当前处于 $x$ 号格子，玩家需要跳到 $x + a _ x$ 号格子上。 如果玩家跳到 $n$ 号格子右侧的位置，称玩家出界；如果玩家**恰好**跳到 $n$ 号格子上，称玩家胜利。这两种情况下玩家都需要停止跳跃。 现在给定格子数量和格子上的整数，你需要求解： 1. 在停止跳跃后，玩家是否胜利。即，玩家是否能够恰好跳到 $n$ 号格子上。 2. 在停止跳跃后，玩家跳跃的总次数。

输入共两行。 第一行为一个整数 $n$，代表格子的数量。 第二行为 $n$ 个整数 $a _ 1, a _ 2, \cdots, a _ n$，代表每个格子上的数字。

输出共两行。 第一行为一个字符串。如果玩家在停止跳跃后恰好跳到 $n$ 号格子上，输出 `Yes`，否则输出 `No`。 第二行一个整数，代表玩家的总跳跃次数。

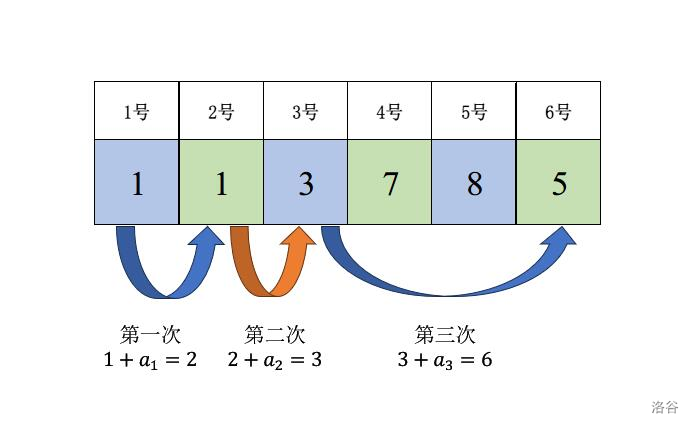
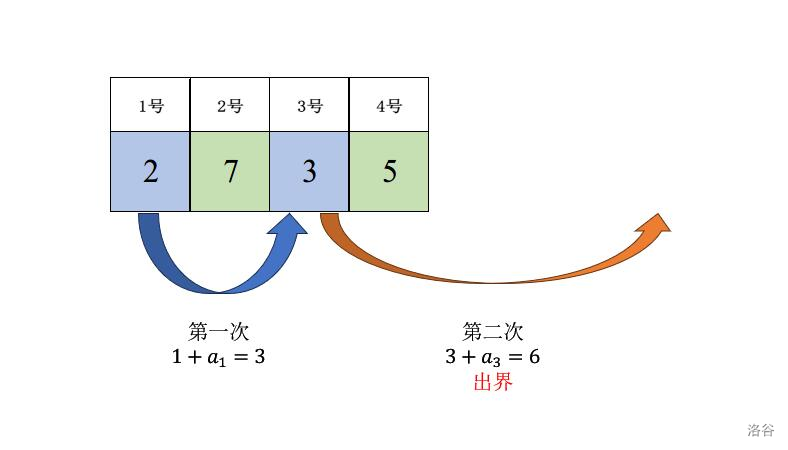
### 样例 1 解释  ### 样例 2 解释  ### 数据规模与约定 对于 $100\%$ 的数据，保证 $1 \leq n \leq 10 ^ 6$，$1 \leq a _ i \leq 10 ^ 4$。 | 测试点编号 | $n$ | 特殊性质 | | :-: | :-: | :-: | | $1$ | $= 1$ | 无 | | $2 \sim 4$ | $\leq 100$ | 无 | | $5$ | $\leq 10 ^ 6$ | $a _ i = 1$ | | $6, 7$ | $\leq 10 ^ 6$ | $a _ i = 2$ | | $8 \sim 10$ | $\leq 10 ^ 6$ | 无 |