T427016 「SFOI Round 1」Game

小 A 和小 B 在一个 $N\times M$ 格的棋盘上玩一个奇妙的游戏。 有一颗棋子，放在左下角 $(1,1)$ 的格子上。从小 A 开始，两人轮流进行任意一种操作： 1. 将棋子向右移动 $1$ 格； 2. 将棋子向上移动 $1$ 格； 3. 将棋子先向右移动 $1$ 格，再向上移动 $1$ 格。 形式化地说，若操作之前棋子的格子为 $(x,y)$，可以选择： 1. 棋子格子变为 $(x,y+1)$； 2. 棋子格子变为 $(x+1,y)$； 3. 棋子格子变为 $(x+1,y+1)$。 当某一方无法进行任何一种操作时，则称这一方失败，而另一方获胜。 请你计算出小 A 第 $1$ 步应该选择哪种操作才可以有必胜策略。特别地，若没有任何一种操作使得小 A 能有必胜策略，则输出 $-1$。 换句话说，我们称小 A 有必胜策略，当且仅当无论小 B 选择哪种操作，其都存在可以获胜的操作方案。

**本题在单个测试点中有多组数据**。 输入共 $T+1$ 行。 第 $1$ 行 $1$ 个整数，表示单个测试点中的数据组数 $T$。 接下来，对于每组数据，输入共 $1$ 行 $2$ 个整数，分别表示棋盘的长宽 $N,M$。

输出共 $T$ 行。 对于每组数据，输出共 $1$ 行 $1$ 个整数，表示小 A 有必胜策略时第 $1$ 步操作的编号。

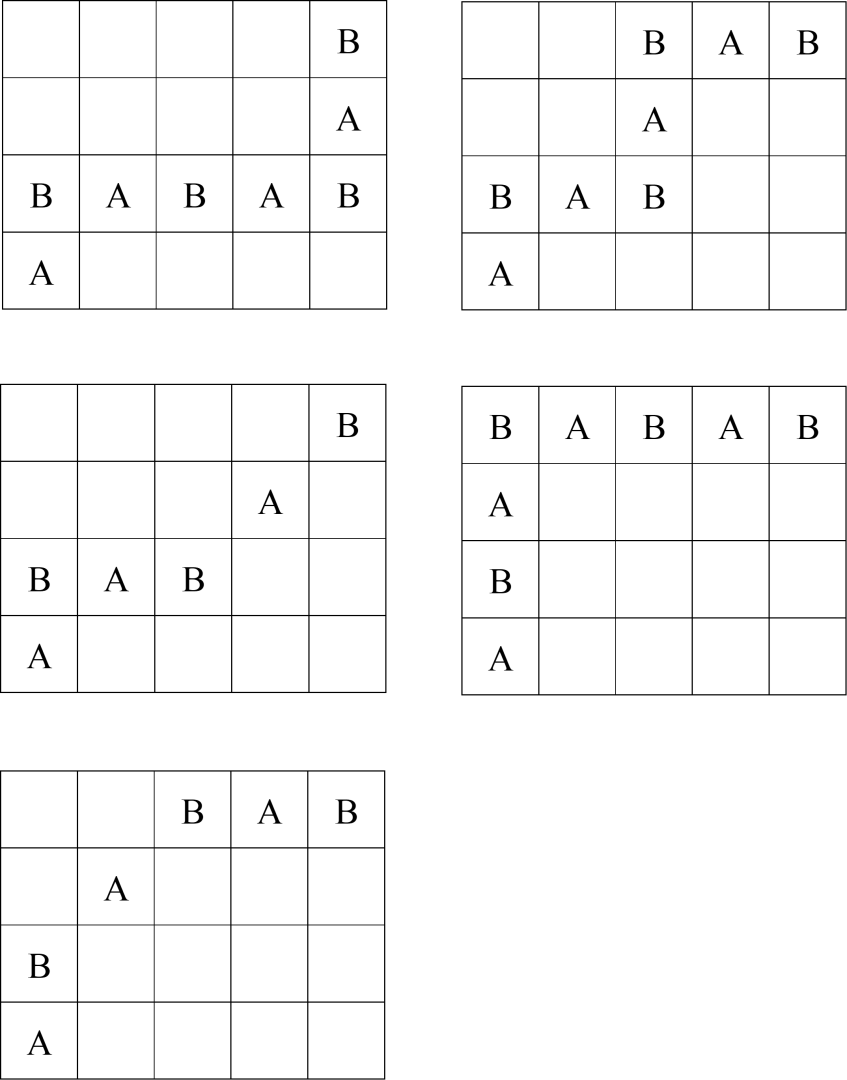
**【样例 1 解释】** 第 $1$ 组数据中，棋盘大小为 $1\times1$。显然此时小 A 无法进行任何一种操作，无解。 第 $2$ 组数据中，棋盘大小为 $4\times5$。不难发现，若小 A 第一步选择向上移动 $1$ 格，小 A 有必胜策略。如下图所示为所有情况下小 A 的必胜策略，其中标有 $\text{A}$ 的格子表示小 A 进行操作前棋子所在的格子，反之同理。  第 $3$ 组数据中，棋盘大小为 $1\times4$。此时小 A 和小 B 均只能向右移动，且恰好小 A 可以获得胜利，即有必胜策略。 --- **【数据范围】** **本题开启捆绑测试**。 对于 $100\%$ 的数据，$1\le T\le10^3$ 且 $1\le N,M\le10^{18}$。 | $\text{Subtask}$ | $N,M\le$ | $\text{Score}$| | :----------: | :----------: | :----------: | | $1$ | $5$ | $20$ | | $2$ | $500$ | $30$ | | $3$ | $10^{18}$| $50$ |