T427018 「SFOI Round 1」Home

你可以点击[这里](/problem/T429617)查看本题强化版。 **本题题面仅供娱乐，请尊重任何一种宗教信仰**。 虔诚的「根式 n 教」信徒小 X 居住在一条无限延伸的一维数轴上，他想要一个家。

在这条数轴上共建有 $n$ 个「原」，即「根式 n 教」的信徒们进行宗教活动「启动」的场所，其坐标分别用 $a_i$ 表示。 每天清晨，小 X 需要从他的家出发，依次前往每一个「原」进行活动。由于每次「启动」需要携带相应的「元素」，而小 X 只能同时携带 $1$ 种「元素」，因此在每次「启动」结束后，他要先从该「原」返回家，找到相应的「元素」，然后才能继续前往下一个「原」进行「启动」。特别的，在最后一次「启动」结束后，小 X 也需要回家。 同时，这条数轴上的任意一个整点处都有一块「神」的宝地，可以用于建造房屋。而每块宝地的售价不同，具体地，坐标为 $l$ 的宝地售价为 $p\times l$，其中 $p$ 为常数。注意，在某些情况下，售价可能为负。 小 X 想要从「神」这里买下一块宝地用来建造他的家。由于他没有很多钱，并且不想走路，他希望每天清晨进行所有「启动」的路程与该宝地的售价之和最小。 特别的，如果有多块符合要求的宝地，小 X 希望他的家的坐标尽可能小。 请告诉小 X 他应当买下的宝地的坐标。 --- **【形式化题意】** 给定序列 $\{a_n\}$ 和常数 $p$，试求当 $\displaystyle\sum_{i=1}^n2|x-a_i|+p\times x$ 尽可能小时整数 $x$ 可取的最小值。

**本题在单个测试点中有多组数据**。 输入共 $2\times T+1$ 行。 第 $1$ 行 $1$ 个整数，表示单个测试点中的数据组数 $T$。 接下来，对于每组数据，输入共 $2$ 行： - 第 $1$ 行 $2$ 个整数，分别表示「原」的数量 $n$ 和宝地的售价参数 $p$； - 第 $2$ 行 $n$ 个整数，分别表示「原」的坐标 $a_i$。

输出共 $T$ 行。 对于每组数据，输出共 $1$ 行 $1$ 个整数，表示小 X 应当买下的宝地的坐标。特别的，若答案的绝对值大于 $10^9$，则输出 $\texttt{No}$。

**【样例 1 解释】** 第 $1$ 组数据中，在这条数轴上，共有 $2$ 个「原」。 | 宝地的坐标 | 「启动」的路程 | 宝地的售价 | 路程与售价之和 | | :----------: | :----------: | :----------: | :----------: | | $\cdots$ | $\cdots$ | $\cdots$ | $\cdots$ | | $-3$ | $2\lvert(-3)-(-1)\rvert+2\lvert(-3)-1\rvert=12$ | $1\times(-3)=-3$ | $9$ | | $-2$ | $2\lvert(-2)-(-1)\rvert+2\lvert(-2)-1\rvert=8$ | $1\times(-2)=-2$ | $6$ | | $-1$ | $2\lvert(-1)-(-1)\rvert+2\lvert(-1)-1\rvert=4$ | $1\times(-1)=-1$ | $3$ | | $0$ | $2\lvert0-(-1)\rvert+2\lvert0-1\rvert=4$ | $1\times0=0$ | $4$ | | $1$ | $2\lvert1-(-1)\rvert+2\lvert1-1\rvert=4$ | $1\times1=1$ | $5$ | | $2$ | $2\lvert2-(-1)\rvert+2\lvert2-1\rvert=8$ | $1\times2=2$ | $10$ | | $3$ | $2\lvert3-(-1)\rvert+2\lvert3-1\rvert=12$ | $1\times3=3$ | $15$ | | $\cdots$ | $\cdots$ | $\cdots$ | $\cdots$ | 不难发现，当宝地的坐标为 $-1$ 时，路程与售价之和最小，为 $3$。 第 $2$ 组数据中，可以证明，路程与时间之和随着宝地的坐标的减小而减小，故答案应为 $-\infty$。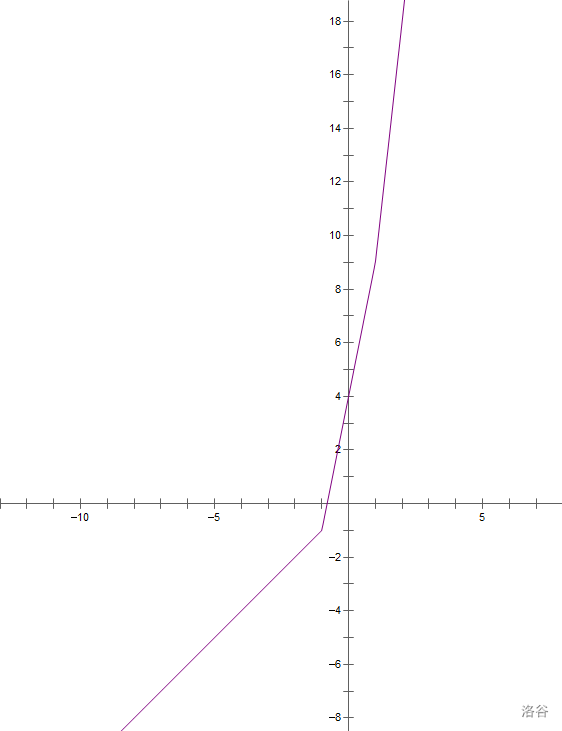如下图为其函数图像的一部分：  --- **【数据范围】** **本题开启捆绑测试**。 对于 $100\%$ 的数据，$1\le T\le5$，$1\le n\le10^6$，$0\le |p|\le10^9$，$0\le |a_i|\le10^6$ 且 $a_i$ 两两不同。 | $\text{Subtask}$ | $n\le$ | $\text{Note}$ | $\text{Score}$| | :----------: | :----------: | :----------: | :----------: | | $1$ | $2$ | $\text{No}$ | $5$ | | $2$ | $100$ | $\text{No}$ | $5$ | | $3$ | $10^3$ | $\text{No}$ | $5$ | | $4$ | $10^4$ | $\text{A}$ | $5$ | | $5$ | $10^4$ | $\text{No}$ | $15$ | | $6$ | $10^6$ | $\text{B}$ | $10$ | | $7$ | $10^6$ | $\text{C}$ | $10$ | | $8$ | $10^6$ | $\text{No}$ | $45$ | - $\text{Note A}$：保证 $p=0$； - $\text{Note B}$：保证 $n$ 为偶数； - $\text{Note C}$：保证 $n$ 为奇数。