T44253 绝美的挣扎

彗星已经分裂，留给三叶的时间不多了。三叶的父亲当机立断，决定以演习的名义疏散全镇居民；然而，糸守湖畔有许多危险设施，必须在彗星落下前妥善处置。为了让更多的人幸存，你能帮助三叶处理好这些设施吗？

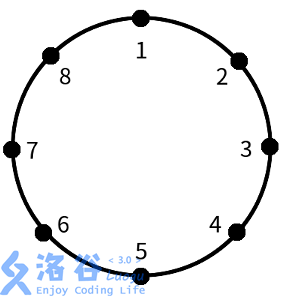
本题中将彗星落下前的糸守湖视为圆形。在糸守湖畔均匀分布着$n$个危险设施，将它们按顺序编号为$1,2,\cdots,n$，如下图。  定义两个设施间的距离为连接这两个设施的圆弧中较短的一条的长度，把相邻两设施的距离定义为$1$单位距离。如上图中，$1$号设施与$2$号设施间的距离为$1$，$1$号设施与$3$号设施的距离为$2$，$1$号设施与$5$号设施的距离为$4$，$1$号设施与$6$号设施的距离为$3$。 这些设施之间存在相互干扰关系，这导致如果控制某一个设施，就不能控制与它距离较近的其他设施。具体地说，每一个设施有一个干扰度$k_{i}(1\le i \le n)$，如果控制$i$号设施，那么就不能控制与$i$号设施的距离**不大于**$k_{i}$的其他设施。例如，在上图中若$k_{1}=2$，则如果控制$1$号设施，就不能控制$2$号、$3$号、$7$号和$8$号设施。 不同设施的危险程度不同。为了描述设施的危险程度，三叶根据相关资料为每个设施评定了危险度，$i$号设施的危险度为$w_{i}$。为了尽可能保障人民群众的生命安全，三叶希望控制的所有设施的危险度之和最大。 现在三叶想求出所能控制的所有设施的危险度之和的最大值，你能帮助她吗？

无

无

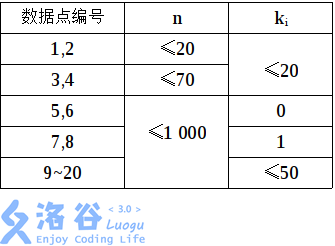
对于10%的数据，满足$n\le 20, k_{i}\le 20$。 对于另外10%的数据，满足$n\le 70,k_{i} \le 20$。 对于另外10%的数据，满足$k_{i}=0$。 对于另外10%的数据，满足$k_{i}=1$。 对于100%的数据，满足$n\le 1000, k\le 50, w_{i}\le 10^{6}, k \le n$。  ------ 样例$1$解释：控制$2,4$号设施。 样例$2$解释：控制$1,3,6$号设施。 样例$3$解释：控制$3,7$号设施。