T467526 [2024迎新马拉松] 回路

给定 $M$ 行 $N$ 列的数字矩阵 $\{a_{i, j}\}_{M \times N}$。矩阵左上角元素的坐标为 $(1, 1)$，右下角坐标为 $(M, N)$。 你要寻找一条从矩阵左上角到右下角，再从右下角到左上角的**回路**。其中，左上角到右下角的那段路径中，每次只能向右或向下走；右下角到左上角的那段路径中，每次只能向左或向上走。矩阵中的每个元素，至多只在回路中出现一次——除了左上角和右下角，任意元素如果出现在了左上角到右下角的那段路径中，就不可以出现在右下角到左上角的那段路径中；反之亦然。 现在，请寻找一条满足以上要求的回路，使得途径元素（左上角除外）的**中位数**最大。

第一行包含两个整数 $M, N$。 接下来 $M$ 行，每行包含 $N$ 个整数，依次描述矩阵的每一个元素。

一个整数，表示最大的中位数。

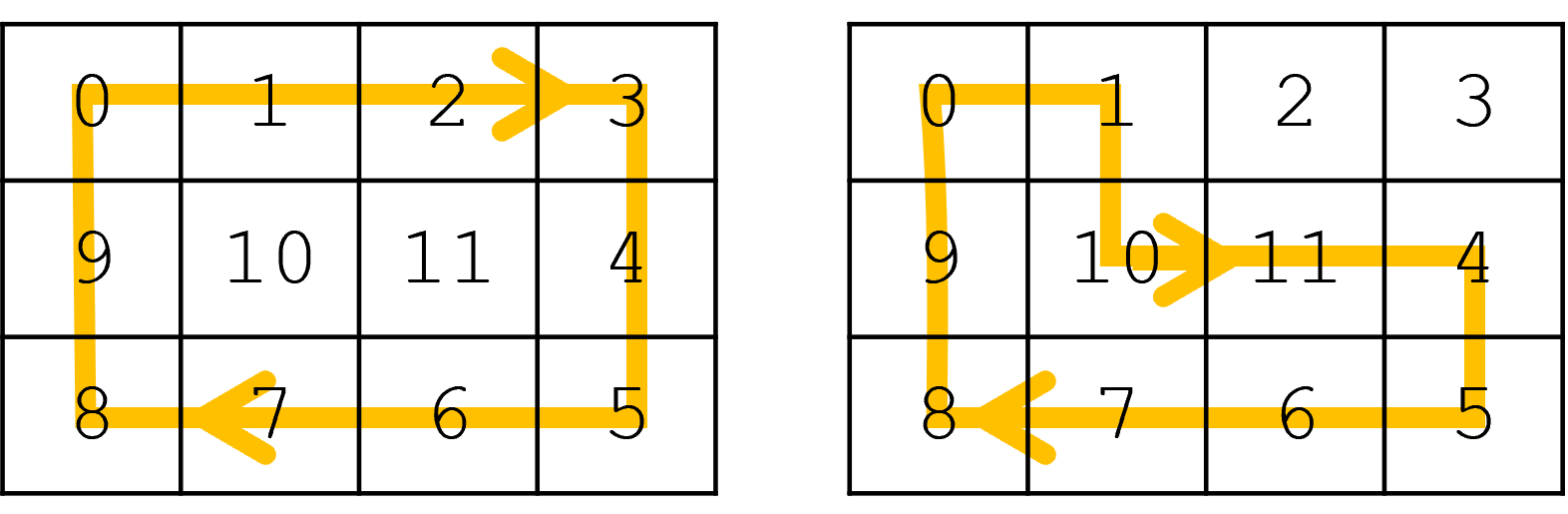
【样例解释#$1$】 下面两个回路中，右边的方案更优。除左上角以外，途径元素有 $1, 10, 11, 4, 5, 6, 7, 8, 9$，其中位数为 $7$。  【数据规模】 本题共有五个子任务，每个子任务捆绑计分： - 子任务一，占分 $10\%$，保证 $M = N = 2$； - 子任务二，占分 $25\%$，保证 $M, N \le 10$。 - 子任务三，占分 $25\%$，保证 $M, N \le 30$，$a_{i, j} \le 1000$； - 子任务四，占分 $20\%$，保证 $M, N \le 30$； - 子任务五，占分 $20\%$，无特殊约定。 对于全部测试数据，保证 $2 \le M, N \le 200$，$0 \le a_{i, j} \le 10^9$ 且 $a_{i, j}$ 互不相同。