T484700 [CZSC 2024] 点

# 请反复确认代码问题不大后再提交！或者直到比赛快结束时再提交！

给定 $n$ 个点，然后再给出 $m$ 个操作。 对于每个操作，给出两个正整数 $x$ 和 $y$，表示将点 $x$ 与点 $y$ 连接。 每个操作结束后你都需要求出有多少个“孤立点”。 如果一个点没有与其他任何点相连接，我们就称该点为“独立点”。

第一行包含两个正整数 $n$ 和 $m$。 接下来 $m$ 行，每行包含两个正整数 $x$ 和 $y$，表示将点 $x$ 与点 $y$ 连接。

输出 $m$ 行，每行一个整数，表示个有多少“孤立点”。

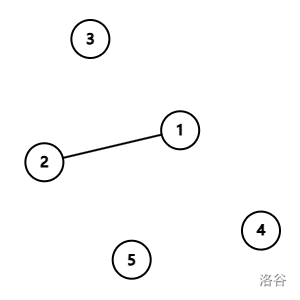
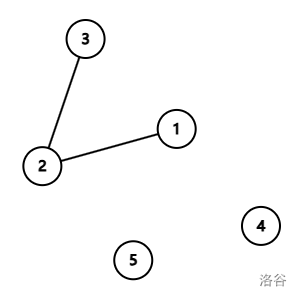
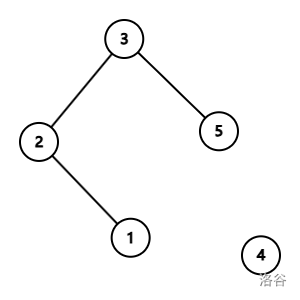
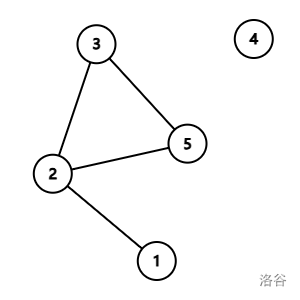
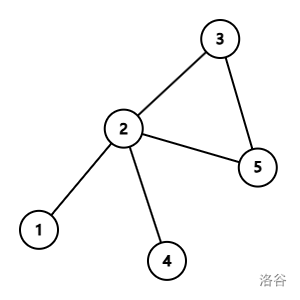
**【样例 1 解释】** 第一次操作，将点 $1$ 与点 $2$ 连接，此时情况如图所示，此时点 $3$, $4$, $5$ 没有与其他点连接，因此孤立点数量为 $3$。  第二次操作，将点 $2$ 与点 $3$ 连接，此时情况如图所示，此时点 $4$, $5$ 没有与其他点连接，因此孤立点数量为 $2$。  第三次操作，将点 $3$ 与点 $5$ 连接，此时情况如图所示，点 $4$ 没有与其他点连接，因此孤立点数量为 $1$。  第四次操作，将点 $2$ 与点 $5$ 连接，此时情况如图所示，点 $4$ 没有与其他点连接，因此孤立点数量为 $1$。  第五次操作，将点 $2$ 与点 $4$ 连接，此时情况如图所示，容易发现没有孤立点。  **【数据范围】** 数据保证不会重复地将两个点相连。对于所有数据，都有 $1\le x,y\le n\le2\times 10^5$，$1\le m \le 10^6$。 |测试点编号|$n$|$m$|其他性质| |-|-|-|-| |$1\sim2$|$=3$|$\le 3$|无| |$3\sim7$|$\le 12$|$\le12$|无| |$8\sim10$|$\le 100$|$=n-1$|无| |$11\sim14$|$\le 100$|$\le 100$|无| |$15\sim17$|$\le 1000$|$\le 5000$|每次操作都满足 $y=x+1$| |$18\sim20$|$\le 1000$|$\le 5000$|每次操作都满足 $x=1$| |$21\sim23$|$\le 2\times10^5$|$\le 10^5$|无| |$24\sim25$|$\le 2\times10^5$|$\le 10^6$|无|