T491047 厕所坑位问题

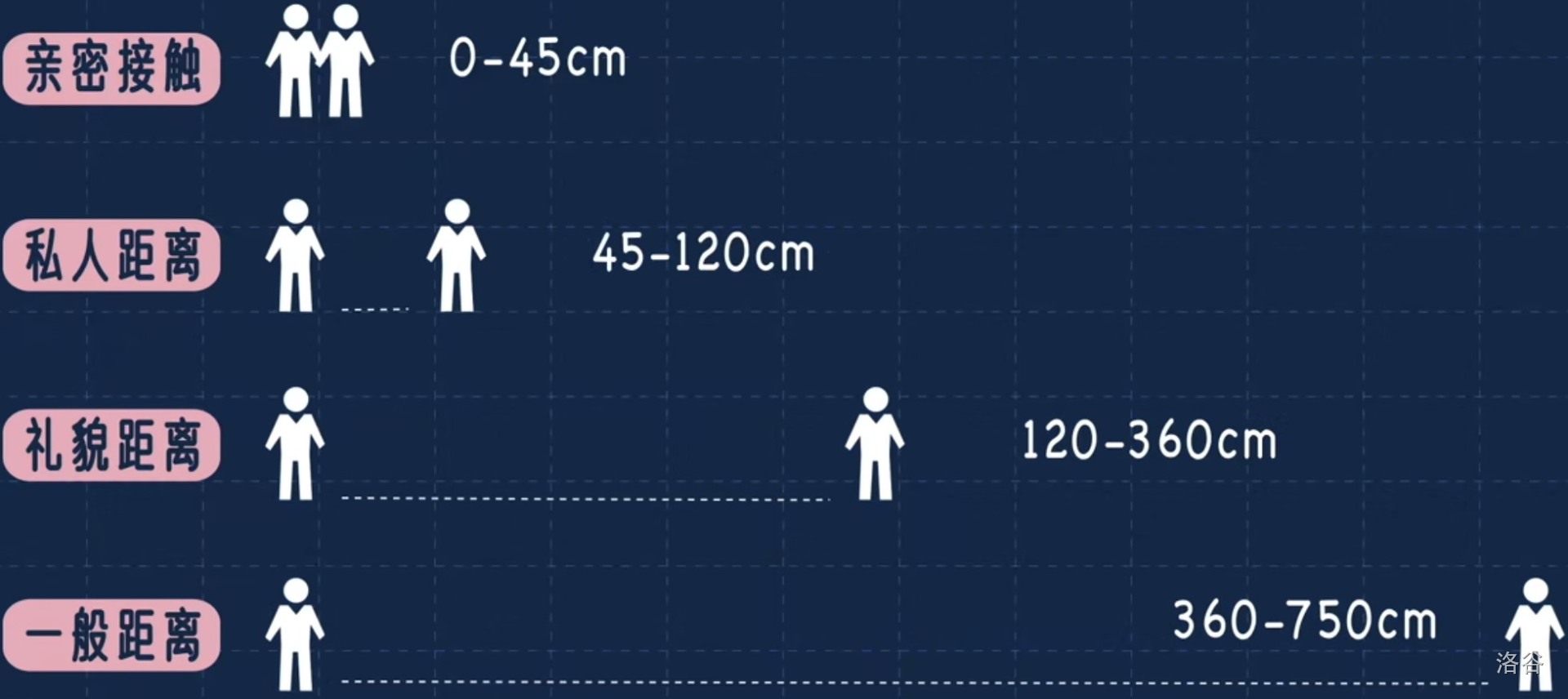
两个男生在上厕所时会由于尴尬而不愿意站在相同坑位上厕所,这被称为"男厕所的泡利不相容定律" ---------- 男厕所的构造 小便区是一排立式坑位,好在有隔板,阻挡隔壁实现,营造私密空间  但是更多的情况是这样的$......$  所以男生通常会里其他人尽可能远 ---------- 社会学研究表明:人的社交分为$4$级,分别为:亲密,私人,礼貌,一般,具体见下图:  亲密距离为$0\sim45\textrm{cm}$,情侣之间才离得这么近$......$ 那两个男生萍水相逢,却在亲密距离件做亲密之事,难免有点$...$[哈子卡西](https://www.baidu.com/s?tn=68018901_3_dg&ie=UTF-8&wd=%E5%93%88%E5%AD%90%E5%8D%A1%E8%A5%BF)$...$如果不说点什么呢,尿声无法掩盖;如果旁边人盯着你呢,你会很不自在;如果互相攀比尿液动力学呢,又有一点变态$......$ 但这是你会发现一个问题,男生的尴尬心态导致了男厕所的坑位利用率显著降低 ------------ 考察一个$4$坑位的厕所  第一个人进来占据$1$号坑  第二个人占据最远的$4$号坑  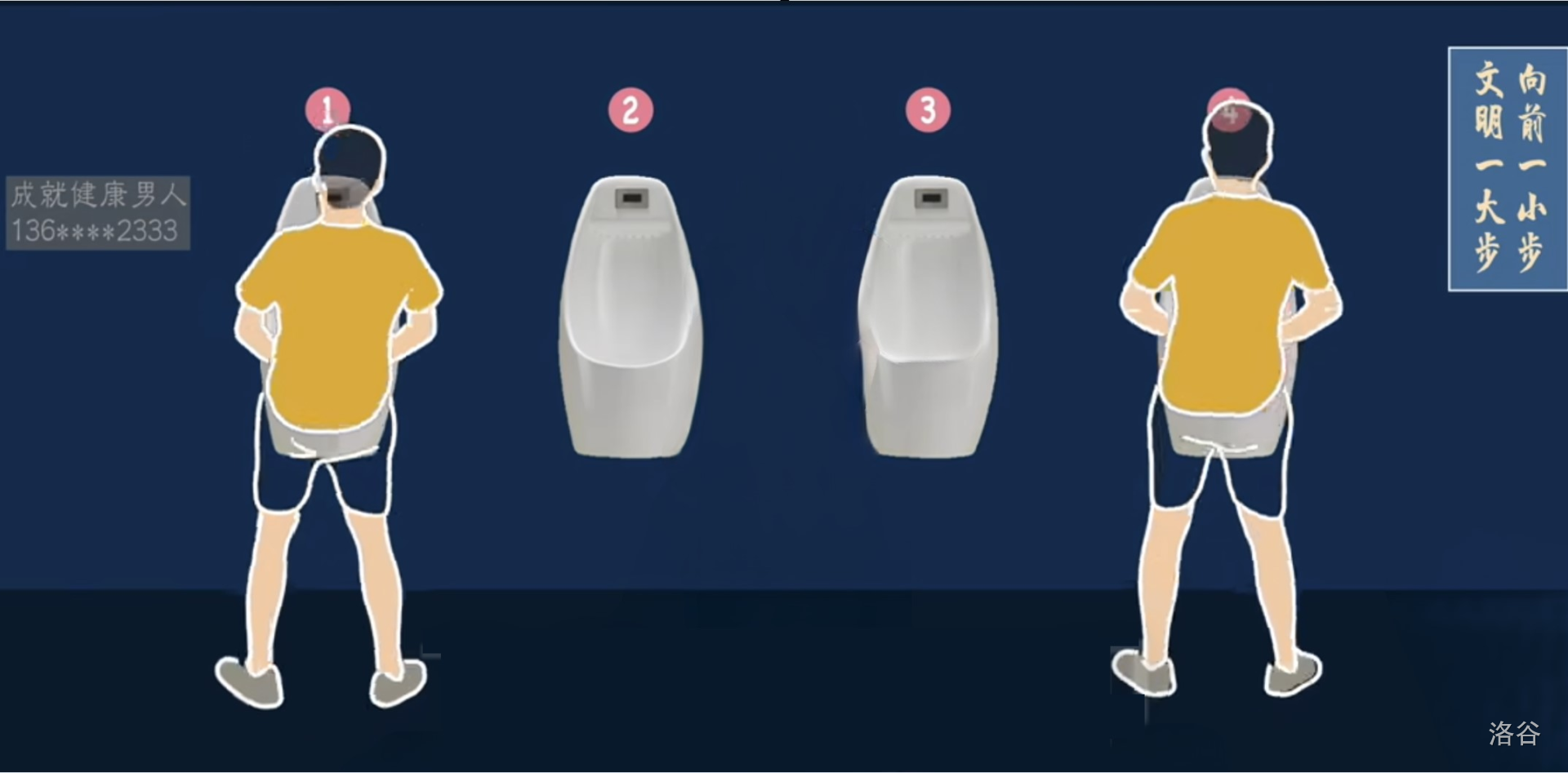第三个人进来就无坑可占了  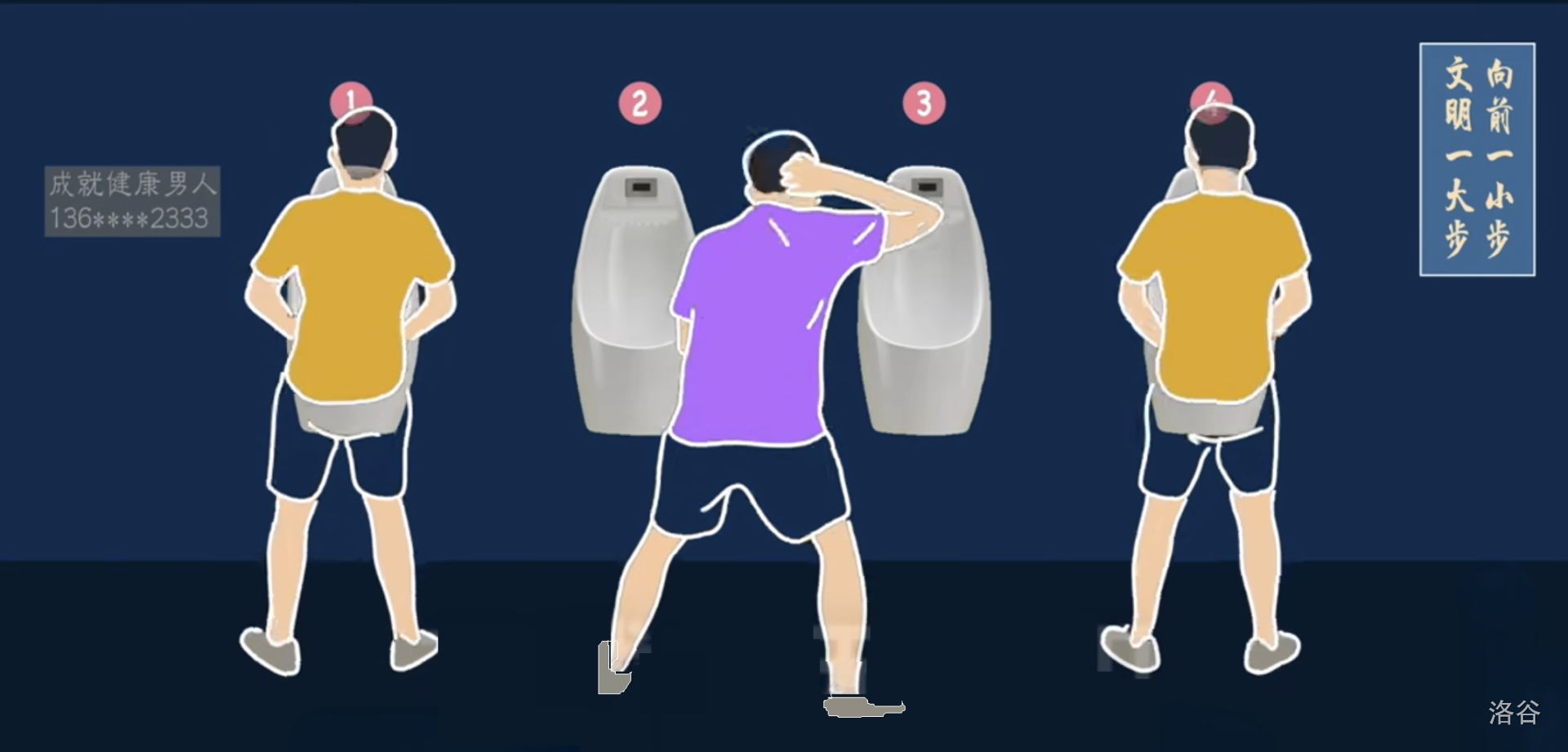因为两边都有人, ------------ 考察一个$7$坑位的厕所  第一个人进来占据$1$号坑  第二个人占据最远的$7$号坑  第三个人进来占据$4$号坑  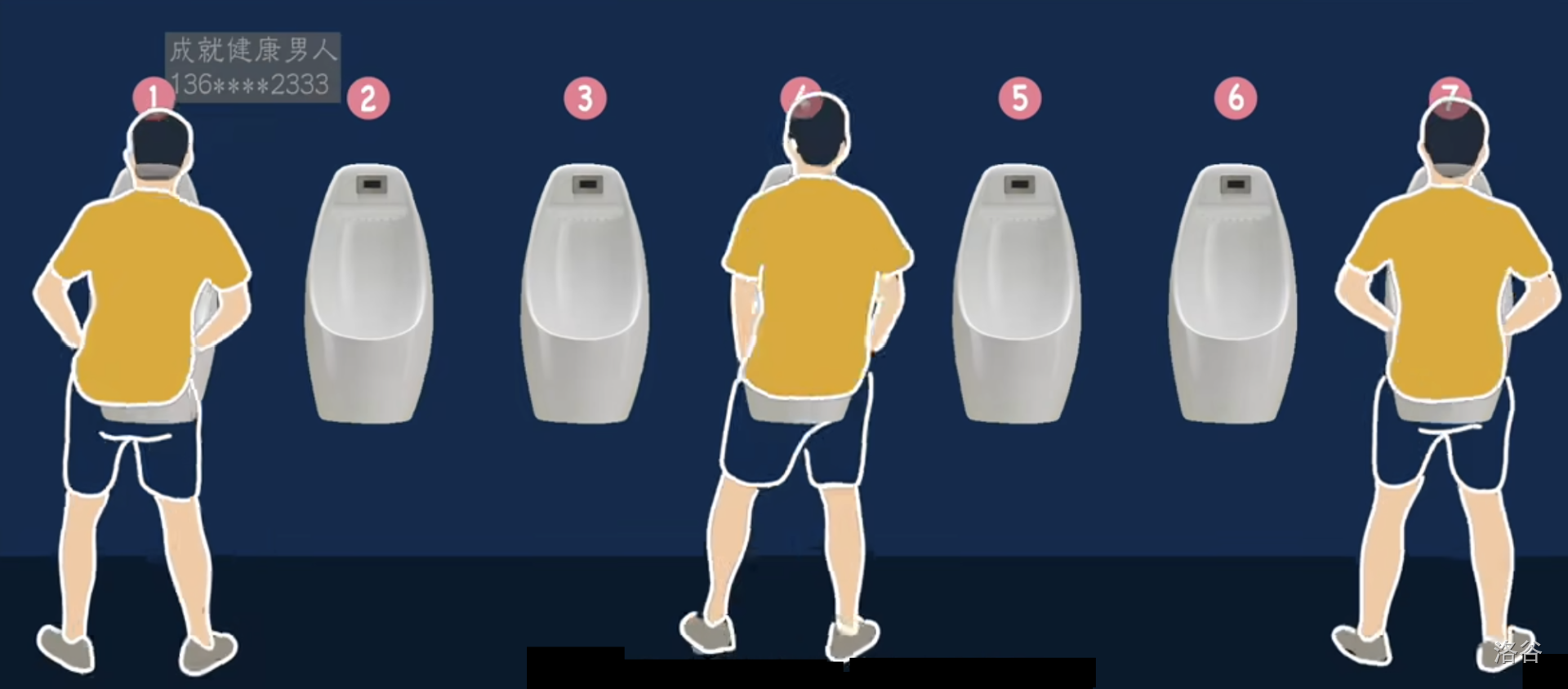第四个人进来就无坑可占了  ---------- 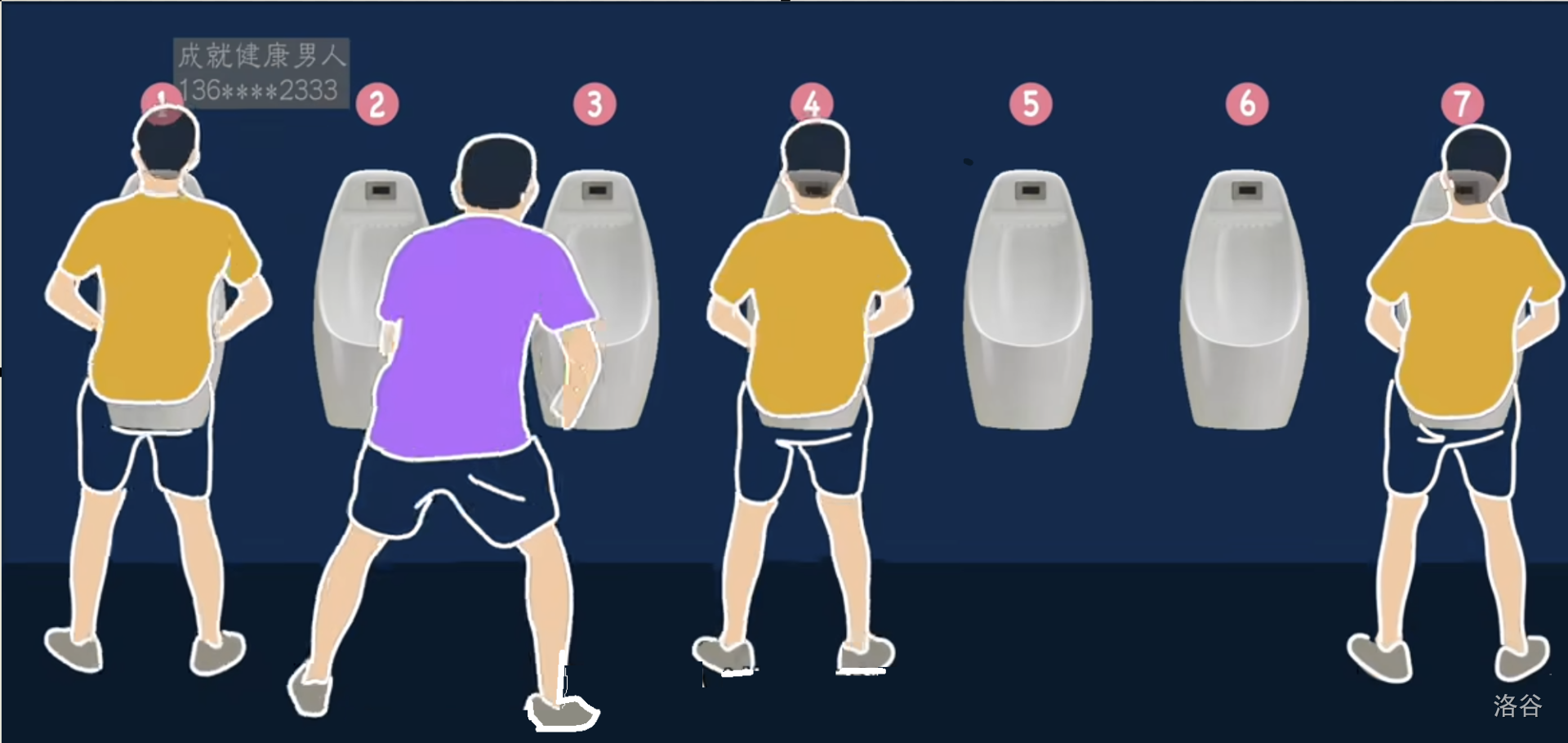同理$13$个坑位的厕所只能容纳$5$个人  ---------- 男生的一点面子,造成了社会资源极大的浪费 ---------- 一个厕所的坑位数量和它能容纳的男生人数满足什么关系呢$?$最优秀的厕所应该设置多少个坑位,才能避免个人尴尬呢$?$ ### 这就是著名的$\Huge\mathcal{\color{#FA4129}男厕尴尬定理}$ 基本模型如下,设一个厕所有$n$个坑位,一群男生先后冲进厕所,占据坑位,设男生上厕所的时间为$∞$,试求该厕所可以同时容纳男生数量$m$与$n$的关系,记为$m=\textrm{f(}n\textrm{)}$ ---------- 下面来给出合理的假设: 男厕第一定律:就近定律 第一个男生为了图方便,总是进入$1$号坑位  男厕第二定律:尴尬定律 男生总是独立进入厕所,后来的男生总会选择离左右男生尽可能远的坑位  男厕第三定律:泡利不相容定律 男生永远不爱着上厕所  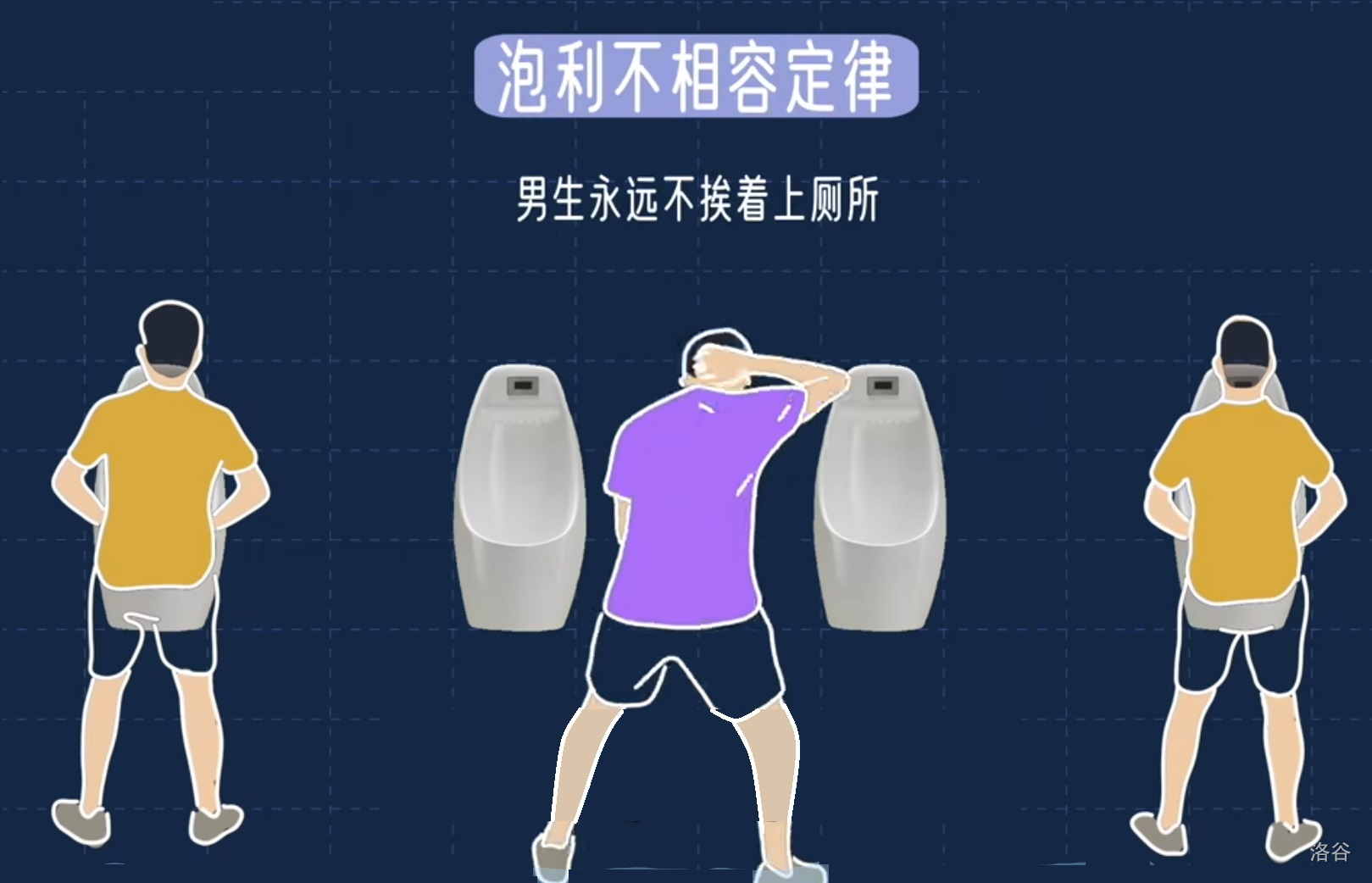下面计算$\textrm{f(}n\textrm{)}$

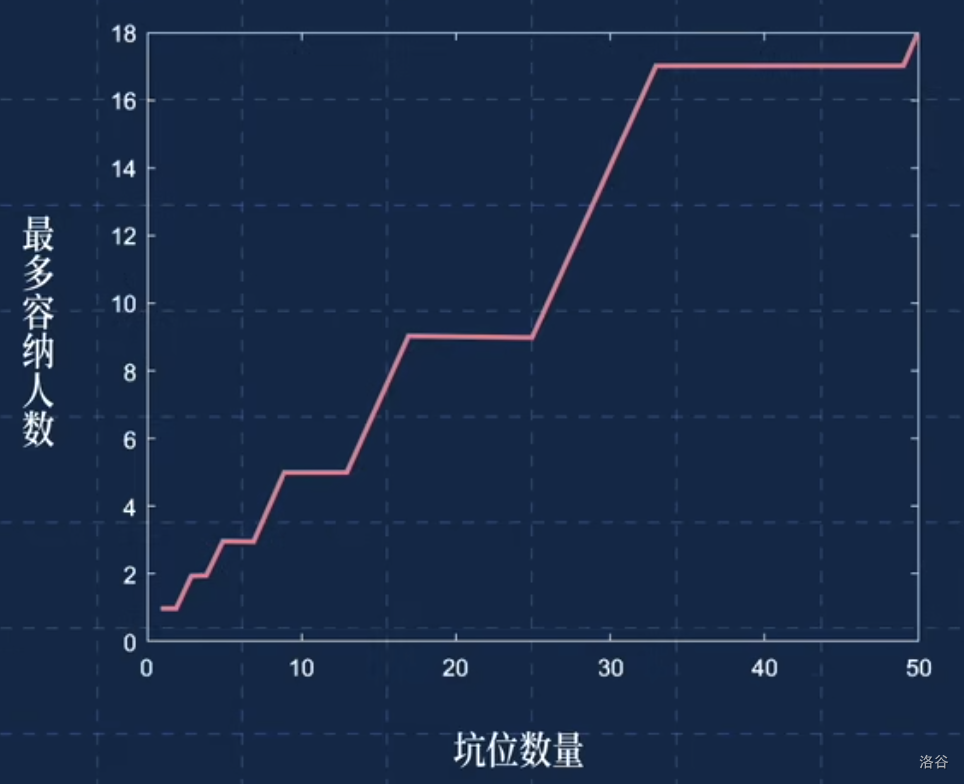
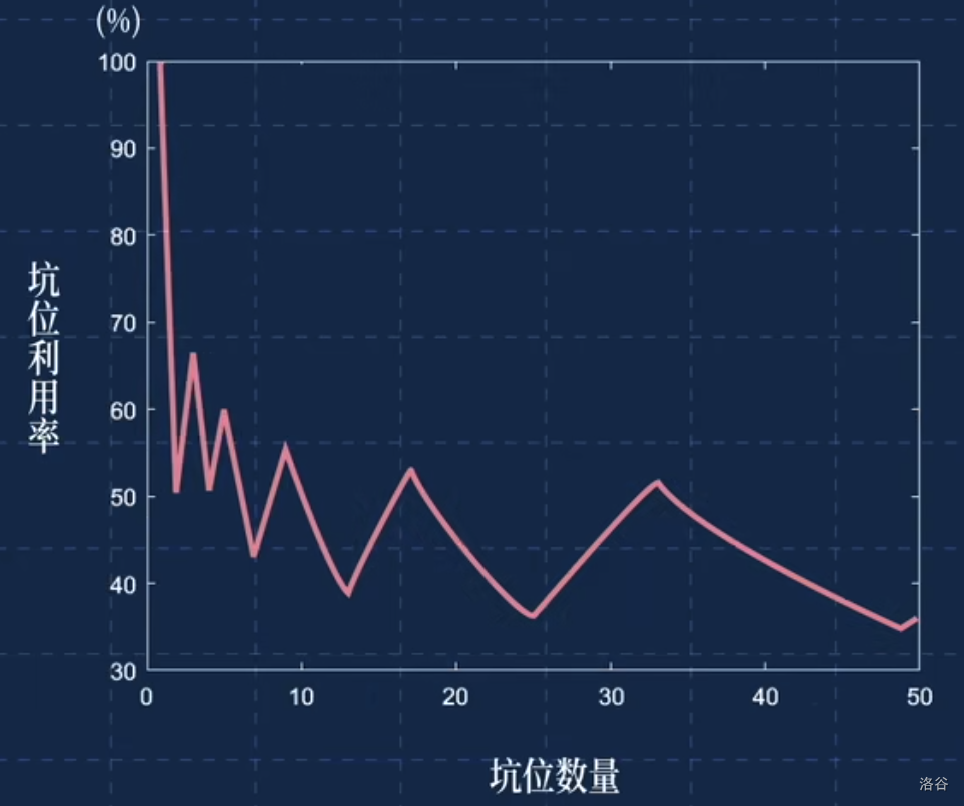
下图为最多容纳人数和坑位数量的关系  下图为坑位利用率和坑位数量的关系  求与男厕坑位相关的问题

第一行,一个整数$T$,表示有$T$组数据 接下来$2\textrm T$行,表示每组数据,其中每组数据为$2$行 每组数据的第$1$行,两个数,分别为$n,Q$,分别为坑位数和询问次数 每组数据的第$2$行,$Q$个字符,表示$Q$次询问,每个字符间用空格隔开($'\textrm M'$表示最多可容纳的人,$'\%'$表示坑位利用率;$'='$表示与坑位$n$容纳人数相等的坑位数量有哪些(用换行隔开,不包括本身,从小到大输出);$'\$'$表示依次输出利用率仅大于$n$且仅小于和大于$n$的坑位数和利用率分别为多少,有换行;$'0'$表示依次输出利用率仅小于$n$且仅小于和大于$n$的坑位数和利用率分别为多少;$'-'$表示与其容纳最多人数相等的坑位中,利用率最低的为几个坑位(包括自己);$'+'$表示与其容纳最多人数相等的坑位中,利用率最高的为几个坑位(包括自己);若没有以上询问则输出$\textrm{I don't know what you want to do.}$)($'\$'$和$'0'$均不包括等于,如果没有利用率小于$/$大于$n$或没有能等于与其最多可容纳的人时,则输出$\textrm{Impossible!}$,如利用率除不尽,则保留百分号后$2$位小数)

对于每一组数据, 先输出数据的组数并换行 对于每一次询问: 先输出询问的内容和$':'$并换行 再把对应的结果输出在下一行(若询问为$'\$'$或$'0'$则输出一行换一行) 再空两行,进行下一次询问的输出 ### $\LARGE\color{red}{\textsf{具体输出格式见样例}}$

#### 样例解释 对于样例$Ⅱ$: $T=2$代表有两组数据 对于第一组数据: $n_1=2,Q_1=7$代表有$2$个坑位,$7$次询问 $Q_1,Q_2,...Q_5$分别为$'M','0','\$','\%'$和$'='$ 第一次询问$'M'$,代表求最多可容纳的人,为$1$人 第二次询问$'0'$,表示求依次输出利用率仅小于$n$且仅小于和大于$n$的坑位数和利用率分别为多少$?$ - 没有利用率仅小于$n$且仅小于$n$的坑位数,故应输出$\textrm{Impossible!}$并换行 - 利用率仅小于$n$且仅大于$n$的坑位数应为$5$,利用率为$\Large\frac{3}{7}$$\times100\%\approx42.86\%$ 第二次询问$'\$'$,表示求依次输出利用率仅大于$n$且仅小于和大于$n$的坑位数和利用率分别为多少$?$ - 利用率仅大于$n$且仅小于$n$的坑位数应为$1$,利用率为$\Large\frac{1}{1}$$\times100\%=100\%$ - 利用率仅大于$n$且仅大于$n$的坑位数应为$3$,利用率为$\Large\frac{2}{3}$$\times100\%\approx66.67\%$ 第四次询问$'\%'$,代表坑位利用率,为$\Large\frac{1}{2}$$\times100\%=50\%$ 第五次询问$'='$,表示求与坑位$n$容纳人数相等的坑位数量有哪些$?$不难得知,只有$1$个坑位能容纳人数与其相等 第六次询问$'-'$,表示与其容纳最多人数相等的坑位中,利用率最低的为几个坑位,为$2$个 第七次询问$'+'$,表示与其容纳最多人数相等的坑位中,利用率最高的为几个坑位,不难得出为$1$个 第二组数据也类似,此处不详细讲述 #### [求解思路](https://www.luogu.com.cn/paste/vr57pjcm) #### 数据规模与约定 对于$10\%$的数据,$T\leq 2, n_i\leq3$ 对于$30\%$的数据,$T\leq 5, n_i\leq10,Q_i\leq4$ 对于$50\%$的数据,$T\leq 25, n_i\leq10^3,Q_i\leq7$ 对于$100\%$的数据,$T\leq 5\times10^3, n_i\leq10^6,Q_i\leq15$