T544015 「YAC Round 13」超级tag料理大赛

 超级tag料理大赛正式开始！！！ 在《东方夜雀食堂》中，特殊顾客们都有自己喜欢的标签，我们称之为 $tag$，例如比那名居天子喜欢 “高级”，雾雨魔理沙喜欢 “菌类”，灵梦则喜欢 “实惠”。 使用不同食材制作出来的料理将会拥有多重的 $tag$，以满足顾客们的多重的喜好需求。

在米斯蒂娅面前有 $n$ 个互不相同的 $tag$，位置从左到右依次为 $p_1, p_2, \ldots, p_n$，这些位置递增且均为正整数，每个位置上的 $tag$ 要么处于 **满足** 状态，要么处于 **未满足** 状态。 米斯蒂娅的面前的料理台上可以放置长段的食材，且可以放置重复一长段的食材， 你可以把每一长段食材看作是一个 **线段**。 米斯蒂娅的料理台初始为空。 现在有 $q$ 次操作，有两种操作： - `1 l r`：将所有 $l \le x \le y \le r$ 且 $x, y$ 均为整数的线段 $[x, y]$ 放到面前的料理台上。 - `2 k`：撤销第 $k$ 次操作中在料理台上添加的所有线段。 在初始情况下和每次操作后，米斯蒂娅可以进行 **任意次** 食材的选择（可以为0次）。 每次从料理台上选出一条线段 $[x, y]$，需要满足米斯蒂娅面前 **位于端点 $x$ 和 $y$ 上** 的 $tag$ 均为 **满足** 状态。 选出一条线段 $[x, y]$ 后，线段区间内所有 **未满足** 的 $tag$ 均会变成 **满足** 状态。 请你在初始情况下和每次操作后，判断米斯蒂娅是否能够找到至少一种合法的食材选择方案使得所有 $n$ 个 $tag$ 都处于 **满足** 状态。 **注意：各组询问之间独立，不会对 $tag$ 造成实际的状态修改**

第一行输入两个整数 $n, q$（$1 \le n, q\le 5\times 10^5$），表示 $tag$ 总数和操作次数。 第二行输入 $n$ 个整数 $p_1, p_2, \ldots, p_n$（$1\le p_i \le 10^9$），表示每个 $tag$ 的位置。 第三行输入 $n$ 个整数 $c_1, c_2, \ldots, c_n$（$c_i = \{ 0, 1 \}$），表示每个 $tag$ 的状态，$c_i = 0$ 表示 **未满足** 状态，$c_i = 1$ 表示 **满足** 状态。 接下来 $q$ 行，每行每行二至三个整数，表示一次操作（$1 \le l < r \le 10^9$，$1 \le k \le q$）。 保证 $p_i$ 互不相同且递增；保证撤销操作合法，且每个操作最多被撤销一次。

输出共 $q + 1$ 行，对于初始情况下和每次操作后，输出一行一个字符串： - 若存在合法的食材选择方案，输出 `Yes`； - 否则，输出 `No`。 你可以输出字符串的任意大小写形式。例如：字符串 `yes`、`YES` 也均会被视为表示存在合法染色方式。

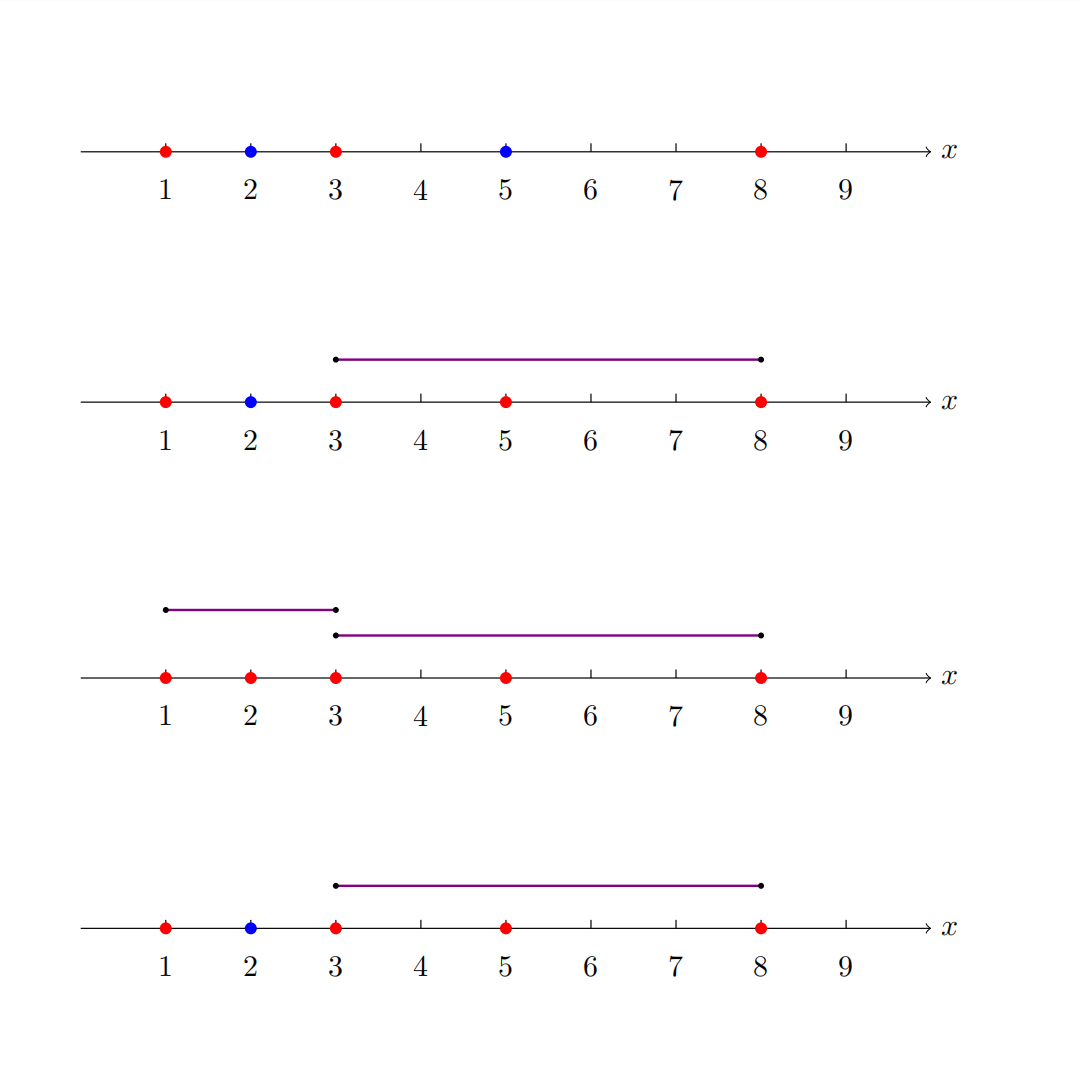
### 样例解释 初始情况下，每个 $tag$ 状态如第一个数轴所示。红色表示满足状态，蓝色表示未满足状态。 显然不是所有 $tag$ 都处于满足状态，因此输出 `No` 。 第一次操作加入了 $[3, 9]$ 区间内的所有线段（包括 $[3, 3]，[3, 4]，[3, 5]，\ldots，[8, 9]，[9, 9]$），可以选择一个满足端点均为满足状态的线段 $[3, 8]$，选出后将 $[3, 8]$ 线段区间内的位于整数点 $5$ 的 $tag$ 变为满足状态。但是，无法使得所有 $tag$ 都处于满足状态，因此输出 `No` 。 如第二个数轴所示。 第二次操作后 **又** 加入了 $[1, 4]$ 区间内的所有线段，此时可以选择线段 $[1, 3]$ 和 $[3, 8]$，使得 $[1, 3]$ 区间内位于 $2$ 的 $tag$ 和$[3, 8]$ 区间内的位于 $5$ 的 $tag$ 变成满足状态。 此时所有 $tag$ 均处于满足状态，因此输出 `Yes`。 如第三个数轴所示。 第三次操作将第二次操作加入的线段全部撤回，此时又回到第一次操作后的形势，因此输出 `No`。