T563941 [202501H] 分队平衡

F 题中的班级搞了一次知识竞赛，然后老师发现每一列同学之间差距过于悬殊，会导致较弱的几列同学参与积极性不高，因此老师想要进行一些调整，使得每一列同学的水平更为接近。

一个班级里的所有同学排成了 $n$ 行 $m$ 列，其中从前往后第 $i$ 行、从左往右第 $j$ 列的同学知识水平为 $a_{i,j}$。 定义一次**调整**的流程如下： - 老师首先会计算每一列同学的知识水平总和，然后对于总和等于最大值或者最小值的所有列，让这些列的同学全部离开座位，并在走廊上按照知识水平从高到低排成一队。 - 接下来，让这些同学按照蛇形顺序坐在空位上。具体地，从前往后坐，同一行内，第奇数行从左往右坐，第偶数行从右往左坐。 给出初始时每个座位上同学的知识水平，计算 $k$ 次调整后每个座位上同学的知识水平。

无

无

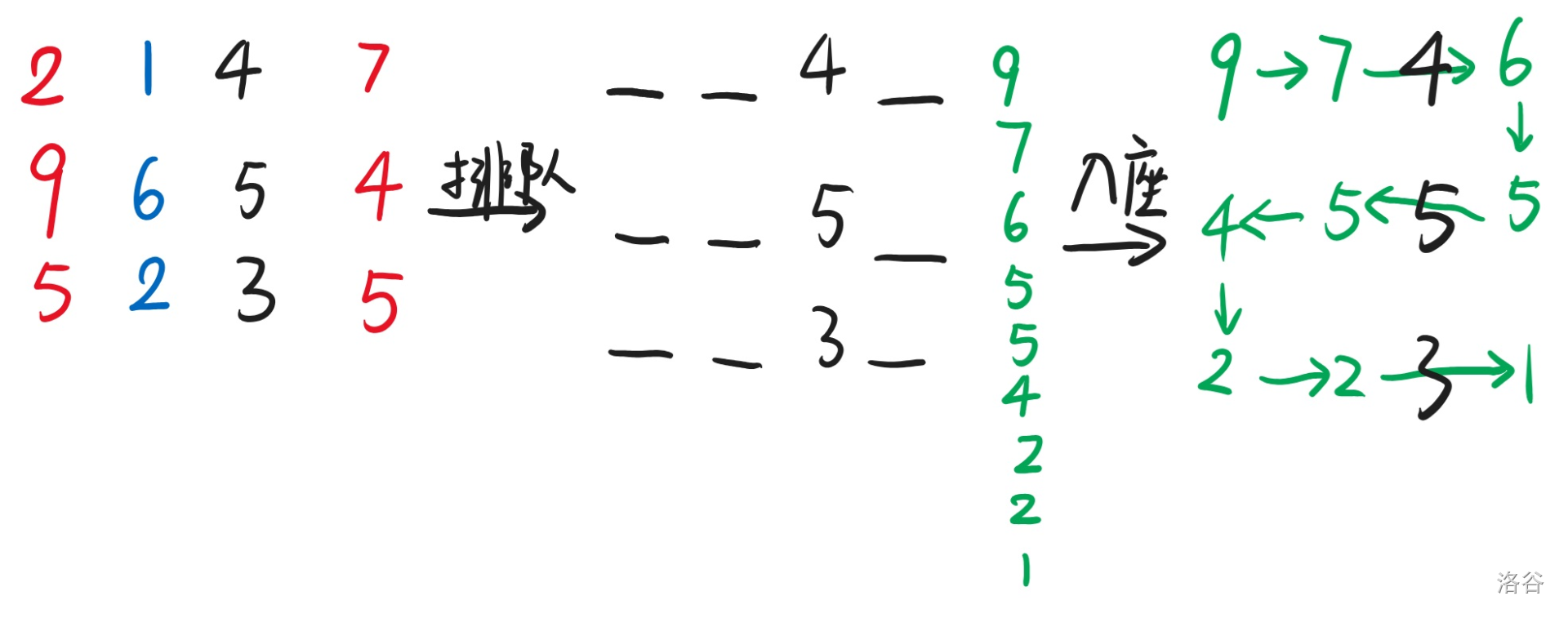
【样例 1 解释】  上图显示了一次调整的流程。 - 左边是原始的座位表，其中标红的两列是知识水平和最高的，标蓝的一列是知识水平和最低的。 - 中间的图为在走廊排队的过程，其中下划线表示产生的空位。 - 右边的图演示了蛇形顺序。 【样例 2 解释】 本样例演示了调整前所有列的总和都已经相等的特殊情况。 第一次调整中，所有同学都离座重新蛇形排列，班级里的座位变成了 $\begin{matrix}40 & 30 \\ 10 & 20\end{matrix}$。 第二次调整中，所有同学都离座重新蛇形排列，但是效果和调整前完全一致。 【数据范围】 对于全体数据，保证 $2 \le n,m\le 50$，$1\le k \le 10$，$1\le a_{i,j}\le 10^9$。（注：$10^9$ 是 $10$ 亿，也就是 $10\ 0000\ 0000$。） 本题共有 $20$ 个测试点，每个测试点 $5$ 分。每个测试点的特殊性质见下表（`Y` 表示保证该性质，`N` 表示不保证）： |测试点编号|特殊性质 A|$a_{i,j}\le$|其他性质| |:-:|:-:|:-:|:-:| |$1,2$|Y|$10000$|$n=2$| |$3\sim 5$|Y|$10000$|| |$6$|Y|$10^9$|$m=2$| |$7\sim 9$|Y|$10^9$|| |$10$|N|$10000$|$n=2$| |$11\sim 13$|N|$10000$|$k=1$| |$14\sim 16$|N|$10000$|| |$17$|N|$10^9$|$k=1$| |$18\sim 20$|N|$10^9$|| - 特殊性质 A：每次调整时只有两列同学离座。