T565978 「PA Mashup #1」等高线

定义好的多边形为各边平行于一条坐标轴，各个顶点都在整点上的简单多边形。 给定 $n$ 个好的多边形，这些多边形的边两两不交，也不接触。 多边形之间可能相互包含。存在一个多边形包含其他所有的多边形，我们称它为**边界**。 定义这张图的**分数**为：选出一个序列 $a_1,a_2,\cdots,a_k$，使得 $\forall 1\le i\lt k$，都有多边形 $a_i$ 包含多边形 $a_{i+1}$（显然 $a_i\neq a_{i+1}$ 必须成立），$k$ 可能的最大值。 在**边界内**添加若干个**好的**多边形，使得添加后，这些多边形的边仍然两两不交，也不接触。最大化添加多边形后的分数，你只需要输出这个分数即可。 可参阅样例解释图片。

第一行一个正整数 $n$。 接下来 $n$ 行描述 $n$ 个好的多边形： 每行先是一个正偶数 $k$，然后是 $k$ 个整数 $x_1,x_2,\ldots,x_k$，表示这个多边形的顶点依次为 $(x_1,x_2),\textcolor{red}{(x_3,x_2)},(x_3,x_4),\textcolor{red}{(x_5,x_4)},\ldots,(x_{k-1},x_k),\textcolor{red}{(x_1,x_k)}$。 按照给定顺序经过多边形的边时，**保证多边形的内部在左侧**。 给出多边形的顺序是任意的。

输出一行一个正整数，表示答案。

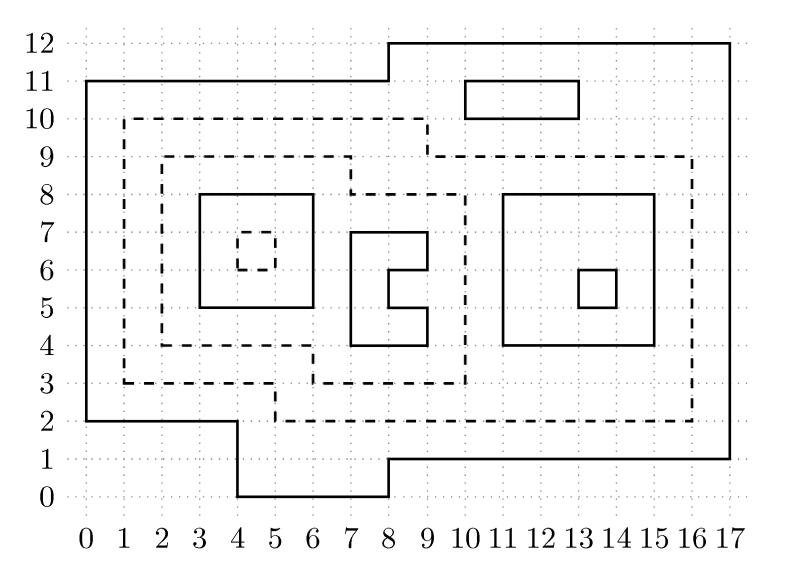
#### 样例解释 如下图，实线代表原图中的多边形，虚线代表添加的多边形。  #### 数据范围 - $2\mid k$，$\sum k\le 5\times 10^4$； - $|x_i|\le 10^8$。