T566563 「PA Mashup #1」台球

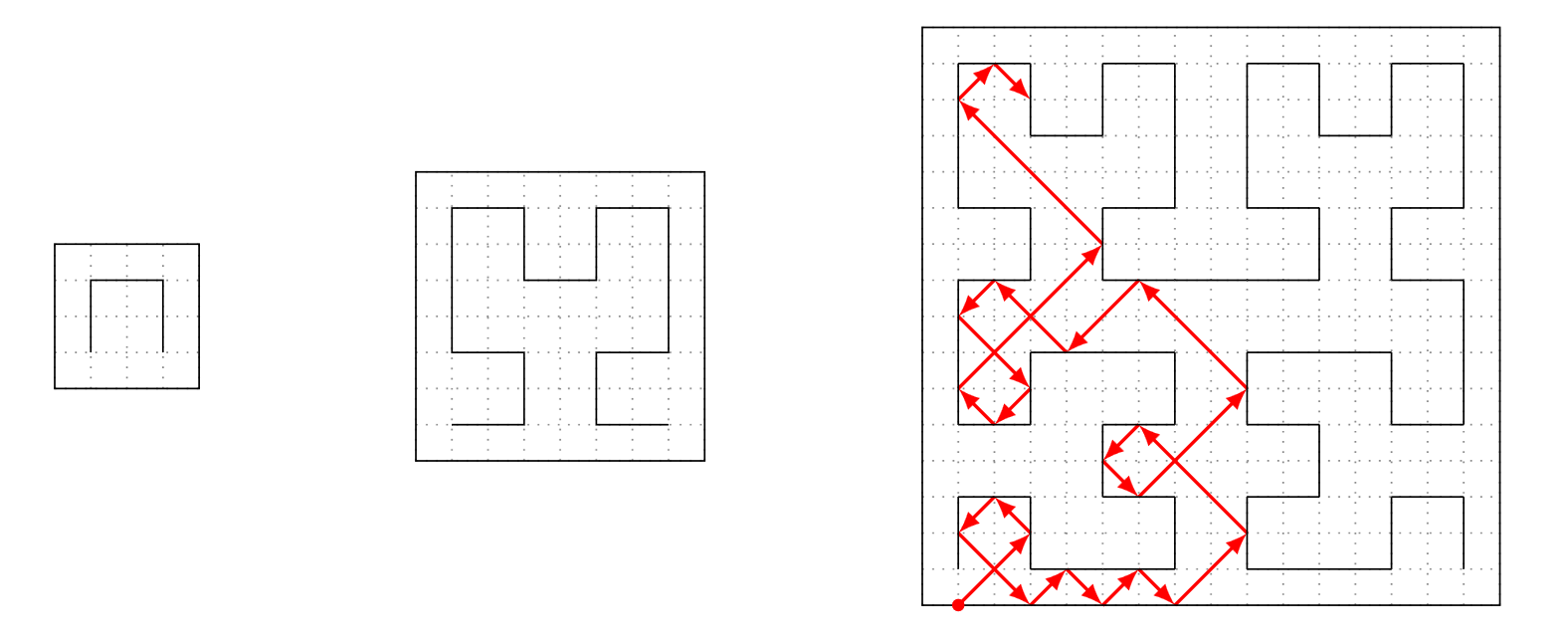
考虑如下的 Hilbert 曲线： $n$ 阶的 Hilbert 曲线的大小为 $2^{n+1}\times 2^{n+1}$。这里，$n\ge 1$。 $n=1$ 时的曲线在下图中给出，而 $n\gt 1$ 时的曲线由四个 $(n-1)$ 阶的曲线组成。左下角的曲线被顺时针旋转了 $90^\circ$，而右下角的曲线则被逆时针旋转了 $90^\circ$，而且在左上与左下、左上与右上、右上与右下的曲线的相接处添加了长度为 $2$ 的额外曲线将它们连为一体。 下图中从左至右分别展示了 $n=1,2,3$ 时的曲线。  令左下角的坐标为 $(0,0)$，右下角的坐标为 $(2^{n+1},0)$，右上角坐标为 $(2^{n+1},2^{n+1})$。 将球视为质点。球从 $(1,0)$ 出发，其速度矢量 $\boldsymbol{v}=(1,1)$。撞到边缘或者曲线上之后，它会反弹，这里的碰撞是**完全弹性碰撞**，也就是垂直于撞击面的速度分量反向，平行于撞击面的速度分量不变。可以证明撞到的一定是一个面，没有撞到角的情况。 $m$ 次询问，每次问球出发 $t_i$ 秒后，球的位置。

第一行两个正整数 $n,m$。 接下来 $m$ 行，第 $i$ 行只有一个整数 $t_i$，描述一次询问。

输出 $m$ 行，每行两个整数表示球的位置。

#### 样例解释 在【题目描述】的图中已经给出。 #### 数据范围 - $1\le n\le 30$； - $1\le m\le 10^5$； - $0\lt t_1\lt t_2\lt \ldots \lt t_m\lt 2^{2(n+1)}$。