T580400 小atom的捉迷藏
题目描述
有$n$个小朋友围着一个三角形的柱子在玩捉迷藏,位置关系如下图所示:
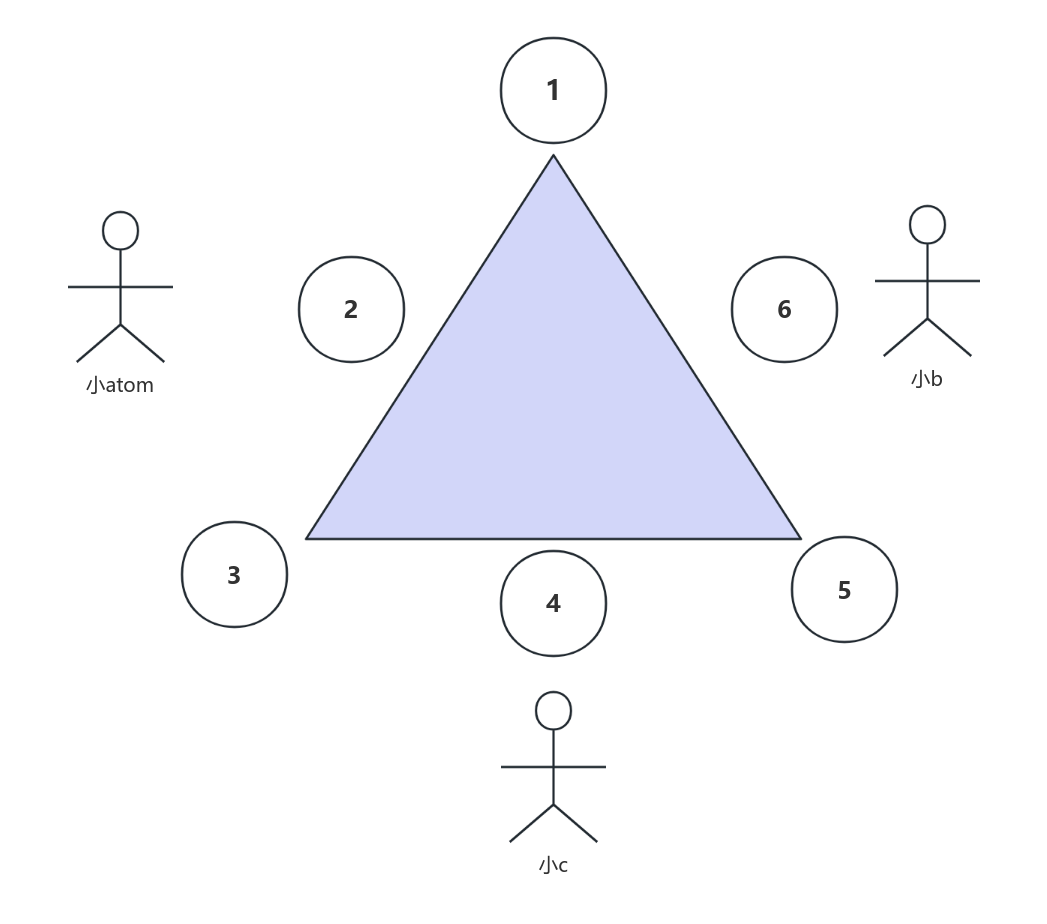
柱子周围有6个位置可以站人,小atom可以看见位于1, 2, 3位置的人;小b可以看见位于3, 4, 5位置的人;小c可以看见位于5, 6, 1位置的人。
每一个位置都可以站任意数量的人。小atom想知道,是否存在一种站立方式,使得小atom、小b、小c分别看到a, b, c个人。
输入格式
每个测试文件均包含多组测试数据。第一行输入一个整数 $T$ ($1 \le T \le 10^4$),代表数据组数,每组测试数据描述如下:
在一行上输入四个整数 $n$ ,$a$ ,$b$ ,$c$ ($1 \le n \le 10^9$;$0 \le a,b,c \le n$),代表小朋友的人数和小atom,小b,小c分别看见多少个人。
输出格式
对于每一组测试数据,新起一行。如果存在一种站立方式,使得小atom,小b,小c分别看到 $a$ ,$b$ ,$c$ 个人,则输入**Yes**,否则输出**No**。
说明/提示
请注意:
60%的测试数据保证$T$, $n$ ,$a$ ,$b$ ,$c$ ($1 \le T \le 10^4$;$1 \le n \le 20$;$0 \le a,b,c \le n$)
40%的测试数据保证$T$, $n$ ,$a$ ,$b$ ,$c$ ($1 \le T \le 10^4$;$1 \le n \le 10^9$;$0 \le a,b,c \le n$)