T580658 小Atom与奶龙

小Atom喜欢拜访奶龙，但他总是迟到。问题是小Atom必须乘渡船过河。于是奶龙决定帮助他的朋友解决这个问题。 这条河是由 $n$ 行和 $m$ 列组成的网格。第 $i$ 行和第 $j$ 列的交点包含数字 $a_{i,j}$ --即相应单元格的深度。**第一列和最后一列**中的所有单元格都与河岸相对应，因此它们的深度为 $0$ 。 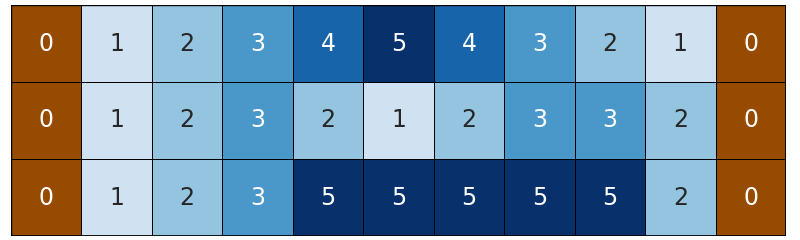 河流可能是这样的。 奶龙可以选择 $(i,1), (i,2), \ldots, (i,m)$ 行，并在其上架桥。在该行的每个单元格中，他都可以为桥安装一个支架。在 $(i,j)$ 单元安装支架的成本为 $a_{i,j}+1$ 。安装支架必须满足以下条件： 1. 必须在单元格 $(i,1)$ 中安装支架； 2. 必须在 $(i,m)$ 单元格中安装一个支撑件； 3. 任何一对相邻支架之间的距离不得大于$d$ 。支架 $(i, j_1)$ 和 $(i, j_2)$ 之间的距离为 $|j_1-j_2| - 1$ 。 只建一座桥是很无聊的。因此，奶龙决定在河上**连续行**建造 $k$ 座桥，即选择一些 $i$ ( $1 \le i \le n - k + 1$ )，在每行 $i, i + 1, \ldots, i + k - 1$ 上独立建造一座桥。请帮助奶龙**最小化**安装支架的总成本。

第一行包含一个整数 $t$ $(1 \le t \le 10^3)$ - 测试用例数。 $(1 \le t \le 10^3)$ - 测试用例的数量。下面是测试用例的说明。 每个测试用例的第一行包含四个整数 $n$ 、 $m$ 、 $k$ 和 $d$ ( $1 \le k \le n \le 100$ 、 $3 \le m \le 2 \cdot 10^5$ 、 $1 \le d \le m$ )--河流的行数和列数、桥数以及支架之间的最大距离。 然后是 $n$ 行， 第$i$ 行包含 $m$ 个正整数 $a_{i,j}$ ( $0 \le a_{i,j} \le 10^6$ , $a_{i,1} = a_{i,m} = 0$ )--河道单元的深度。 保证所有输入数据集的 $n \cdot m$ 之和不超过 $2 \cdot 10^5$ 。

对于每个测试用例，输出一个数字 - 支架安装的最低总成本。