T582974 L2-3 朋友悖论

“我没几个朋友，但我的每个朋友都拥有许多朋友。”孤独的 Zaoly 如是抱怨道。 幸运的是，作为校长，你清楚掌握着 Zaoly 所在的大学里的朋友关系网。你想用数据安慰他，告诉他：你不是一个人。

已知该校共有 $N$ 个人。校园中的朋友关系网可以表示为一个无向图，有 $N$ 个顶点和 $M$ 条边，其中第 $i$ 条边连接顶点 $U_i$ 和顶点 $V_i$，表示 $U_i$ 和 $V_i$ 是朋友。图中保证没有重边和自环。~~不要猜 Zaoly 的顶点编号！~~ 如果一个人，他（她）的朋友数量**严格少于** $k$，且他（她）的每个朋友都拥有**至少** $k$ 个朋友，那么这个人会很孤独。 请注意：“每个朋友都……”应当理解为“**没有**朋友**不**……”。也就是说，如果一个人没有朋友，我们认为“每个朋友都……”这个命题也成立。 对于每个 $k = 1, 2, \ldots, N$，有多少人会很孤独？

输入第一行给出一个正整数 $T$（$\le 10^4$）表示测试用例的个数。 每个测试用例第一行给出两个整数 $N$ 和 $M$（$1 \le N \le 2 \cdot 10^5$，$0 \le M \le 2 \cdot 10^5$，$M \le \frac {N \cdot (N - 1)} 2$）表示顶点数和边数。 接下来 $M$ 行中，第 $i$ 行给出两个整数 $U_i$ 和 $V_i$（$1 \le U_i, V_i \le N$，$U_i \ne V_i$）表示第 $i$ 条边连接的顶点。对于一切满足 $1 \le i < j \le M$ 的整数 $i$ 和 $j$，都有 $U_i \ne U_j$ 或 $V_i \ne V_j$，并且 $U_i \ne V_j$ 或 $V_i \ne U_j$。 保证所有测试用例的 $N$ 值之和与 $M$ 值之和都不超过 $2 \cdot 10^5$。

对于每个测试用例，在一行中输出 $N$ 个整数，表示 $k = 1, 2, \ldots, N$ 时孤独的人数，中间用 $1$ 个空格分隔。

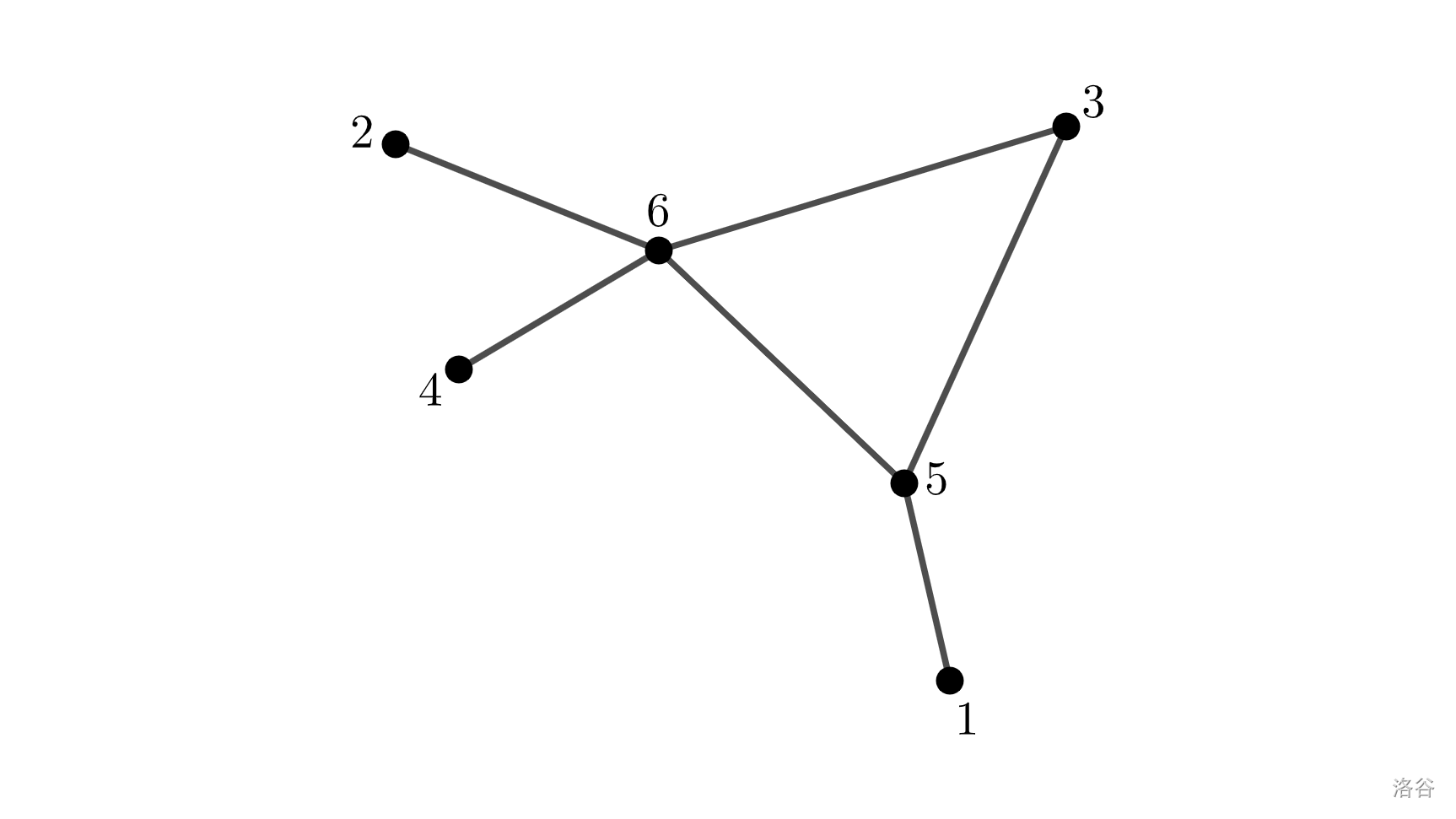
在第一个样例中，二人彼此依靠，无一落单。 在第二个样例中，堂堂三人，竟无一对朋友，可谓孤独至极！ 在第三个样例中，几乎每两个人都是朋友，只有一对例外（$2$ 和 $3$），因此这两个人偶尔也会感到孤独。 第四个样例有点复杂，直接上图：  当 $k = 2$ 时，$1$、$2$、$4$ 会很孤独。 当 $k = 3$ 时，$1$、$2$、$3$、$4$ 会很孤独。 当 $k = 4$ 时，$2$、$4$ 会很孤独。