T678364 三角形晶格

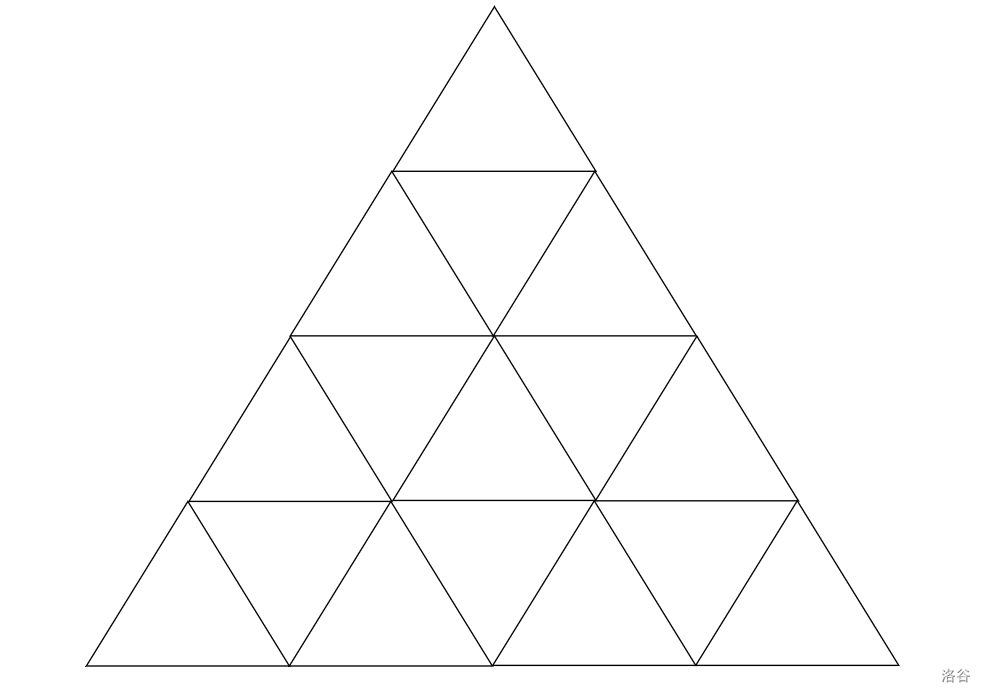
有一个全由**正三角形**组成的晶格图，设有一个 $n$ 阶三角形晶格，第 $i$ 层 $(i \in [1, n])$ 有 $2i - 1$ 个正三角形。 其中第 $i$ 层的第 $j_1$ 个三角形 $j_1 \equiv 1 \pmod{2}, j_1 \in [1, 2i-1]$ 是一个尖角朝上的正三角形； 其中第 $i$ 层的第 $j_2$ 个三角形 $j_2 \equiv 0 \pmod{2}, j_2 \in [1, 2i-1]$ 是一个尖角朝下的正三角形。 下图是一个 $n = 4$ 的三角形晶格实例:  在这个三角形中设最大的正三角形边长为 $4$，共有： $16$ 个边长为 $1$ 的正三角形； $7$ 个边长为 $2$ 的正三角形； $3$ 个边长为 $3$ 的正三角形； $1$ 个边长为 $4$ 的正三角形。 所以 $n = 4$ 的三角形晶格中共计 $16 + 7 + 3 + 1 = 27$ 个正三角形。 给出三角形晶格的阶数，求该三角形晶格中正三角形的总数。 由于答案可能很大，请输出答案对 $10^9 + 7$ 取余后的结果。

一行一个整数 $n$， 表示三角形阶数。

一个整数，表示 $n$ 阶三角形晶格中正三角形的总数。

对于 $20\%$ 的数据， 有 $1 \le n \le 800$， 对于 $40\%$ 的数据， 有 $1 \le n \le 2000$， 对于 $60\%$ 的数据， 有 $1 \le n \le 1.5 \times 10^6$。 对于 $100\%$ 的数据，有 $1 \le n \le 10^9$。