U115094 「ACSL2019-2020 #4」Patolli
题目背景
本题来自 [ACSL](http://www.acsl.org/) 系列比赛2019-2020年的第四轮编程试题。
英文题面及数据点 $1-10$ 来自由举办方 [ASDAN](http://www.seedasdan.org/acsl/) 举办的中国赛区比赛。
**本题仅供练习,本人与上述两组织无关系。**
鉴于主办方给出的中文翻译并不靠谱,本题翻译由上传者 @zxp_oistream 自行翻译。
题目描述


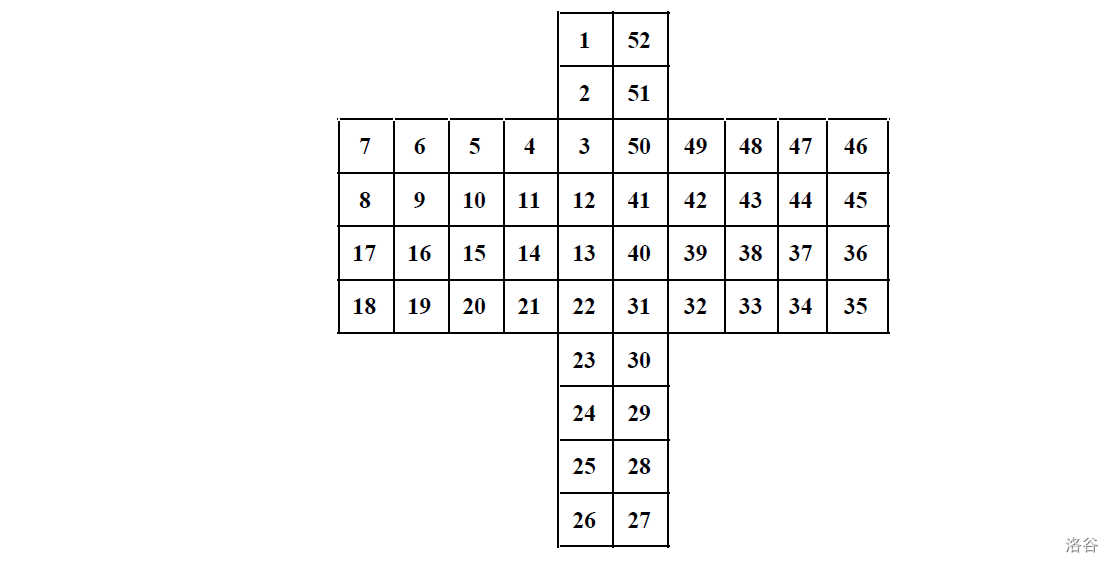
输入格式
输入有一行。
- 前三个整数为对方棋子位置。
- 此后三个整数为本方棋子位置。
- 此后一个整数 $r$,表示本次游戏中掷骰子的次数。
- 此后 $r$ 个整数,依次为每次掷骰子得到的点数。
所有整数之间以空格分隔。
输出格式
输出有一行,为按照升序排序好的整数,表示上述骰子投完后我方在棋盘上的棋子的位置(以格子序号输出)。
如果我方(在上述骰子投完后)没有棋子在在棋盘上了,则输出 `GAME OVER`。
说明/提示
### 测试点分布
本题所有数据中,$r \leq 100$。
| 测试点 | 时空限制 | 分值 | 备注 | Subtask |
| ----------- | ----------- | ----------- | ----------- | ----------- |
| $1 - 2$ | $1$s / $256$MB(下同),原题并没有时间 / 空间限制。本题时空限制开到上传者比赛时写的大常数 STL 代码的两倍以上(还算是仁慈吧。。) | $5$ | 原题样例,本题样例 | $1$ |
| $3 - 5$ | | $5$ | 原题样例 | $1$ |
| $6 - 10$ | | $15$ | 原题数据,后 $5$ 个测试点并没有公布正确答案,本题以我手算正确的结果为答案。 | $2$ |
### 样例解释

对于样例 $\#1$,三个对方的棋子分别在 $4$,$14$,$24$ 号格子。三个我方棋子在 $1$,$8$,$12$ 号格子。共掷了 $6$ 次骰子。
1. 一开始,位于 $1$ 号格子的棋子最靠后(所在格子编号最小),所以它将按照骰子的点数前移 $6$ 格,到 $7$ 号格子。$7$ 是个质数,所以它可以再向前移动 $6$ 格,但是 $8$ 号格子被占用了(有我方棋子),所以它只能停留在 $8-1=7$ 号格子。
2. 骰子掷出的下一个点数是 $3$。这会使 $7$ 号格的棋子移动到 $10$ 号格子。此时最靠后的棋子变成了位于 $8$ 号格的棋子。
3. 下一个点数是 $5$,$8$ 号格的棋子前移到 $13$ 号格子。$13$ 是个质数,所以它还可以前移 $6$ 格,但是 $14$ 号格被占用,它只能停留在 $14-1=13$ 号格子。
4. 下一个点数是 $1$,现在最靠后的棋子在 $10$ 号格子。它会前移到 $11$ 号格子。$11$ 是个质数,所以它还可以前移 $6$ 格,但是 $12$ 号格被占用,它只能停留在 $12-1=11$ 号格子。
5. 下一个点数是 $5$ ,最靠后的是位于 $11$ 号格子的棋子。它将前移到 $16$。$16$ 是个大于 $4$ 的完全平方数,所以它可以后退 $6$ 格,但是 $14$ 号格被占用,所以它停在 $14+1=15$ 号格子。
6. 最后一个点数是 $6$ ,在 $12$ 的棋子会移动到 $18$,但是在这过程中经过了至少一次横向移动($16$ 号格至 $17$ 号格)后接一次纵向移动($17$ 号格至 $18$ 号格),所以这枚棋子将必须落在这条路径上编号是 $6$ 的整倍数的格子。它最终落在 $18$ 号格子($\dfrac{18}{6} = 3$)。
因此,三枚棋子分别在 $13$,$15$,$18$ 号格子。