U125546 JZOI 4311 统一天下
题目背景
有一天,小H成为了一个国家的国君。。。
题目描述
从前有两个国家$W_1$, $W_2$。国家$W_i$($i∈ \{1,2\})$有$n_i$座城市,这$n_i$座城市由$n_i-1$条双向道路相连。任意一个国家的内部都是连通的。一个国家的两个点之间存在唯一的最短路,两个点的距离是这条最短路上边的数目。(也可以理解为道路的长度均为$1$。) 注意$W_1$和$W_2$并不联通。
有一天,$W_1$的军队在小H的带领下一举攻破了$W_2$,建立了大一统的政权$W$。为了使全国连通,小H决定在$W_1$的某个点和$W_2$的某个点之间新修建一条路,使得$n=n_1+n_2$个点两两组成的$\dfrac{n(n-1)}{2}$个点对的距离和最小。
小H请你帮帮他,算一下这个最小距离。
输入格式
第一行两个整数$n_1,n_2$。
接下来$n_1 - 1$行,每行两个整数$x,y$,代表在$W_1$中的$x,y$两座城市间有一条路。
接下来$n_2 - 1$行,每行两个整数$x,y$,代表在$W_2$中的$x,y$两座城市间有一条路。
输出格式
一行一个整数,表示最小的和。
说明/提示
#### 样例解释
连接 $W_1$ 的 $3$ 号点和 $W_2$ 的 $4$ 号点可以取得最小值。
#### 关于数据
本题数据并非全是官方数据,但保证合法。
$ n, m \le 3 × 10^5$
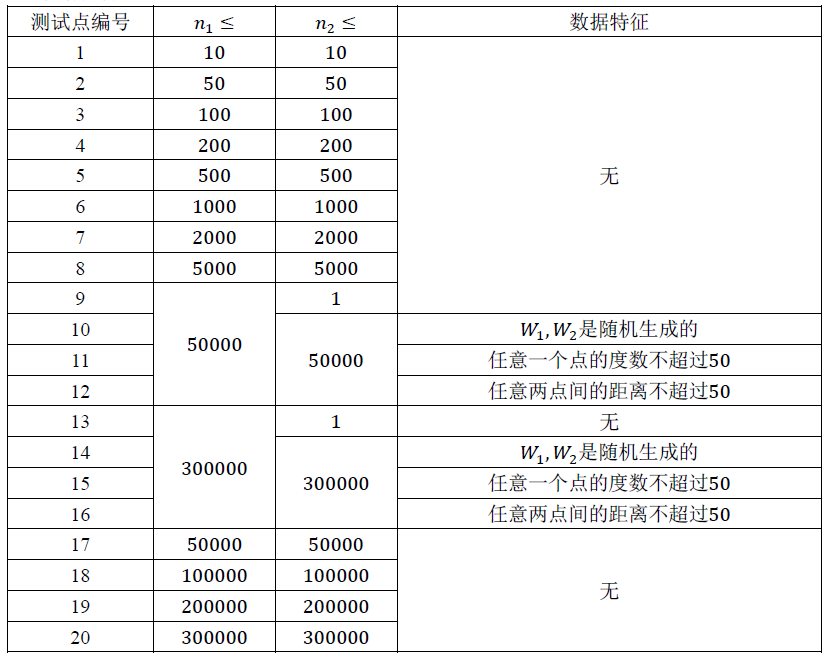
### 如何做对这道题
#### [题解](https://www.cnblogs.com/wondering-world/p/13446257.html)