U138346 统治王国

某日午后，$Seaway$一觉醒来，发现自己穿越到了蒟蒻王国，并当上了蒟蒻王国的国王......在反穿越失败后，$Seaway$接受了这个事实，并尝试着统治这个王国......

蒟蒻王国一共有$N$个城市，$N-1$条可以双向通行的链接两个城市的道路，每条道路的长度相等。并且，蒟蒻王国的所有城市间两两可达。$Seaway$的王宫位于$1$号城市。为了统治蒟蒻王国，$Seaway$需要出宫巡视；并且，为了展现自己对底层人民的关怀，$Seaway$只关心自己到达了多少“偏远城市”，偏远城市的定义是：只有一条路与外界相连的城市。但是，贵为一国之王，$Seaway$的巡视路线要遵循王室的标准，在每座他停留的城市，他只能选择两种方式继续巡视： ​ 第一种：如果当前城市不是偏远城市，那么去往当前城市下辖的任意一个偏远城市。这里的下辖指：除了王宫方向之外的所有方向。 ​ 第二种：如果当前城市是偏远城市，那么他可以向着王宫的方向巡视不超过$K$个城市。 ​ 特别地，因为$1$号城市是王宫所在，所以即便1号城市只有一条路与外界相连，它也不属于偏远城市。 ​ 作为蒟蒻王国的总会计师，$Seaway$要你帮他规划出：他此次巡视最多能巡视多少偏远城市。 ​ 由于答案可能较大，请输出答案对$998244353$取模的结果。

从文件$kingdom.in$中读入数据。 第一行包括两个整数$N,K$， 第二行包含$N-1$个整数，第$i$个整数$f_i$表示第$i+1$号城市的上级城市。输入保证$1$号城市是所有城市的上级。

输出到文件$kingdom.out$中。 仅一行一个整数，表示可以巡视的最多偏远城市数对$998244353$取模的结果。

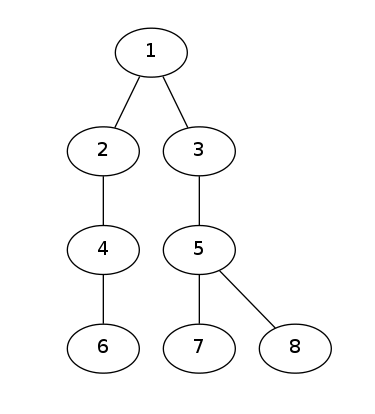
【**样例1解释**】 王国地图：  在这个王国，$Seaway$可以选择如下巡视路线：$1-2-1-5-3-7-4-6$。 【**样例2解释**】 王国地图：  在这个王国，$Seaway$可以选择如下巡视路线：$1-7-5-8$。 【**数据范围**】 对于$4\%$的数据，有$f_i=i-1$。 对于另$4\%$的数据，有$f_i=1$。 对于另$12\%$的数据，有$1\le N\le 10$。 对于另$40\%$的数据，有$1\le N\le 2\times 10^3$。 对于全部数据，有$1\le K