U140603 树的平均

$Seaway$太菜了。当大佬们都在爆切插头DP，计算几何，反演，Matrix-Tree的时候，$Seaway$连最基本的搜索都打不对...... 菜归菜，$Seaway$还是有一些基本常识的：他知道，对于一棵有根树，可以进行两种不同的遍历方式：DFS和BFS。这两种遍历方式在遍历过程中会分别生成两种序列：DFS序和BFS序。$Seaway$惊奇地发现：对于两棵不同的树，它们的DFS序有可能相同，它们的BFS序同样有可能相同。$Seaway$大呼绝妙，并觉得这里大有文章可做。

现在，$Seaway$给出一个DFS序和一个BFS序。他想知道，在符合这两个限制条件的所有有根树中，树的高度的平均值。即：假如有$N$棵不同的树具有这组$DFS$序和$BFS$序，且它们的高度分别为：$h_1,h_2,\cdots,h_n$，那么请你求出下式的值： $$ \frac{\sum_{i=1}^{i=N}h_i}{N} $$ 这里的树的高度是指：树的最深深度。

从文件$average.in$中读入数据。 第一行一个整数$N$，表示树的节点个数。 第二行有一个$1-N$的排列，描述树的DFS序。 第三行有一个$1-N$的排列，描述树的BFS序。

输出到文件$average.out$中。 一行输出一个实数，保留三位小数。表示答案。你能够获得本测试点的分数，当且仅当你的答案与标准输出的差的绝对值小于等于$0.001$。

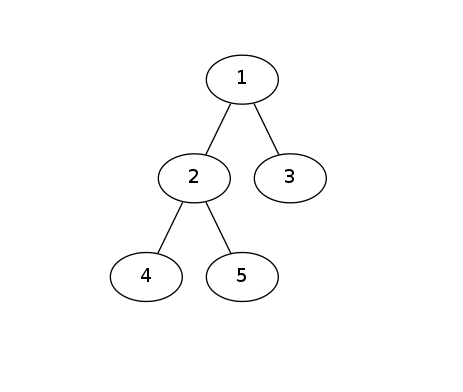
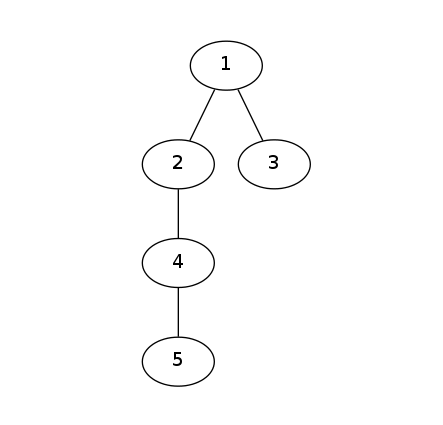
【**样例1解释**】 符合这两个序列限制的树有两种，其形态如下：   【**数据范围**】 对于$20\%$的数据，$1\le N\le 10$。 对于$ 40\%$的数据，$1\le N\le 100$。 对于$85\%$的数据，$1\le N\le 2000$。 对于全部数据， 有$1\le N\le 3\times10^5$。