U149791 正多边形变换
题目背景
《代数学方法(第一卷)基础架构》——李文威 著
P109:§4.3 - 例 4.3.5
题目描述
给定一个正 $n$ 边形,中心与坐标原点重合,一个顶点在 $x$ 轴正半轴上,从这一个顶点开始,逆时针顺次标为 $P_0,P_1,P_2,\dotsm,P_{n-1}$ 。标 $x$ 轴为 $0$ ,从 $x$ 轴开始顺时针标这个正多边形的对称轴为 $1,2,\dotsm,n-1$ 。
给定以下两种操作(下文中的正整数 $k$ 满足 $0 \leqslant k < n$):
- 操作 $0$ :将图形逆时针旋转 $\frac{2 \pi k}{n}$ 弧度
- 操作 $1$ :将图形关于标号为 $k$ 的对称轴对称
可以保证,对于任意 $m$ 次操作,总可以找到一种操作,使得这一次操作后的顶点排布与那 $m$ 次操作后的顶点排布相同。请你求出这一种操作。
输入格式
共 $m+1$ 行:
第 $1$ 行:两个整数 $n$ 和 $m$ ,表示图形的边数 $n$ 和操作的次数 $m$ (用空格隔开)
第 $2$ 至 $m+1$ 行:两个整数 $op$ 与 $k$ ,表示这一次操作的类型 $op$(为 $0$ 或 $1$)与操作中出现的变量 $k$ (用空格隔开)
输出格式
共一行:
第一行:两个整数 $op$ 与 $k$ ,表示要求的操作的类型 $op$(为 $0$ 或 $1$)与操作中出现的变量 $k$ (用空格隔开)
说明/提示
数据范围:
对于 $100\%$ 的数据,$3 \leqslant n \leqslant 114514$,$2 \leqslant m \leqslant 1919810$
------------
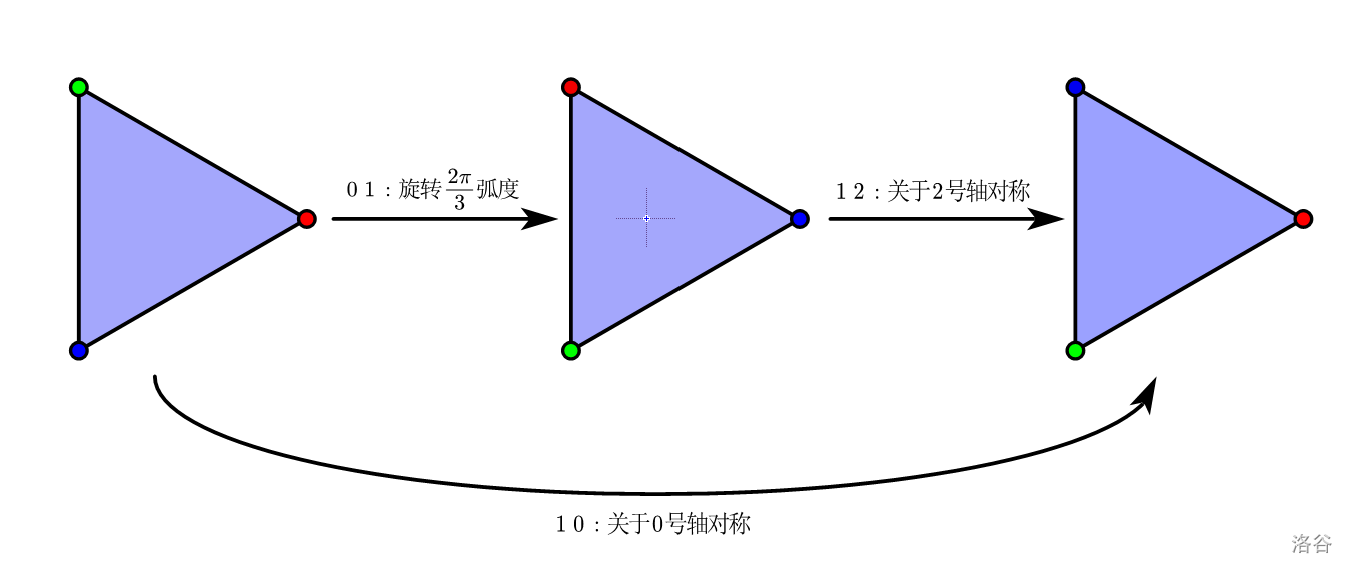
样例1的图解(红色点为 $P_0$,绿色点为 $P_1$,蓝色点为 $P_2$):