U201758 包装纸问题

由于需要去打osu!，在C城的礼品包装纸生产工厂工作的小a找到了你，希望你帮他完成今天的工作。

小a的工作内容很简单，就是用一张样板来生产包装纸。 工厂有一个存在电脑里的包装纸样板，每次生产礼品包装纸都是从里面截出一部分生产。这个样板基本形状为一个长方形的网格，长方形的长方向共有 $m$ 列，它们的宽度分别为 $a_1, \cdots, a_m$ 。宽方向有 $n$ 行，宽度分别为 $b_1, \cdots, b_n$ 。在网格的每个格子里都有各不相同的花纹图案，生产包装纸的时候会一并印制在纸上。 由于C城的客户喜欢方方正正的包装纸，所以你生产的包装纸只可以是沿着格线切割下来的一个矩形。为了区分不同的包装纸种类，我们认为两张包装纸不同当且仅当至少有一种花纹为其中一张包装纸所独有。 现在小a已经介绍完了工作内容，而你的第一个任务是：生产可以用这张样板生产的所有不同的包装纸各一张。为了顺利完成这个任务，现在需要完成一个程序，来帮你计算： 1. 所有可以生产出来的不同包装纸种类数 $N$ ； 2. 生产他们各一个需要的材料面积之和 $S$ 。 由于答案可能很大，你只需要输出 $N, S$ 对 $10 ^ 9 + 7$ 取模的结果。

第一行两个整数 $m, n$ 。 第二行 $m$ 个整数 $a_1, \cdots, a_m$ 。 第三行 $n$ 个整数 $b_1, \cdots, b_n$ 。

一行两个整数，表示 $N, S$ 对 $10 ^ 9 + 7$ 取模的结果。

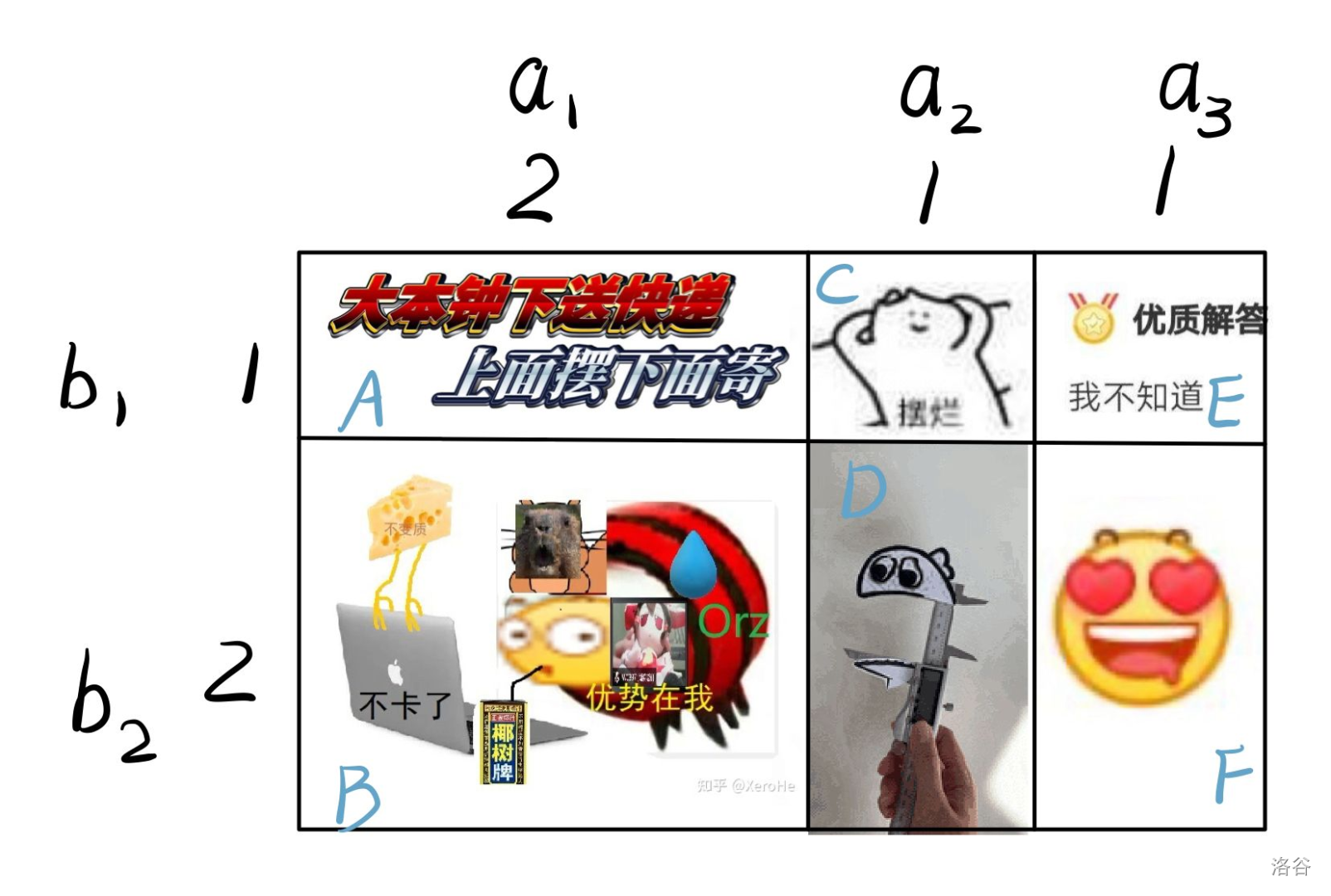
## 样例解释 对于样例1，其样板形状如下：  所有可以截出的不同包装纸为： $A(2), B(4), C(1), D(2), E(1), F(2)$ $AB(6), AC(3), BD(6), CD(3), CE(2), DF(4), EF(3)$ $ACE(4), BDF(8)$ $ABCD(9), CDEF(6)$ $ABCDEF(12)$ 面积之和为：$2 + 4 + 1 + 2 + 1 + 2 + 6 + 3 + 6 + 3 + 2 + 4 + 3 + 4 + 8 + 9 + 6 + 12=78$ ## 数据范围与约定 本题分Subtask测试，你需要通过Subtask里的全部测试点以获得相应分数。 | 子任务编号 | $m, n$ | $a_i, b_i$ | 分值 | | :--- | :---- | :--- | :--- | | 0 | $m, n \leqslant 100$ | 无特殊限制 | 10 | | 1 | $m, n \leqslant 10000$ | 无特殊限制 | 40 | | 2 | 无特殊限制 | 无特殊限制 | 50 | 对于所有数据， $1 \leqslant m, n \leqslant 5 \times 10^6, 1 \leqslant a_i, b_i \leqslant 10^9$ 。