U204706 国际象棋
题目背景
一个阳光明媚的午后,又到了 Nickel 和 Windy 茶会的时间,但 Windy 还没有来,Nickel 无聊的在家中走来走去。这时她发现了小时候玩过的国际象棋。她看着国际象棋上的格子,喜欢数学的她突然想到了一个问题。
题目描述
在一个没有边界的国际象棋棋盘上,一个国王在坐标为 $(0, 0)$ 的格子上。现在可以让国王走不超过 $n$ 步(不移动国王视为走 0 步,也是合法的),问最终国王可以落在多少种不同的位置?
Nickel 想和 Windy 在茶会上讨论这个问题。为了测试问题的难度,她现在要考考你,你能解决 Nickel 的问题吗?
Nickel 给你了一张图片提示,以防你不知道国王的移动规则。下图中王冠即为国王所在位置,红色的格子即为国王走一步可以到达的位置。
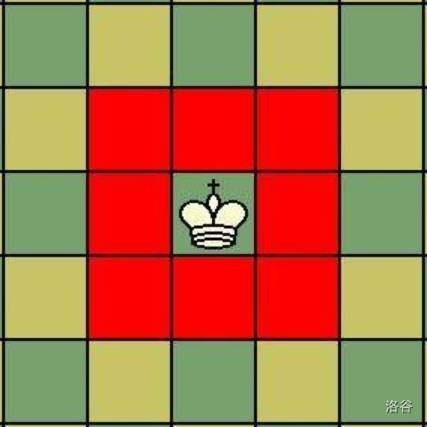
输入格式
输入仅一行,一个整数 $n$。
输出格式
输出一个整数,表示问题的答案。
说明/提示
**样例解释**
国王走不超过一步可以到达的格子有:
$(-1, 1),\,(0, 1),\,(1, 1),\,(-1, 0),\,(0,0),\,(1, 0),\,(-1, -1),\,(0, -1),\,(1, -1)$。
**数据范围**
$0 \le n \le 10^8$。