U208225 与和树 Bitwise AND
题目背景
与:指一种位运算。
和:指两样东西之间的并列关系。
树:指构成的是树。
ckj 决定给 jyn 送一份独特的 ~~OI 风格的~~情人节礼物。
题目描述
ckj 决定送 jyn 一棵深度为 $n$ 的满二叉树(根节点深度为 $1$),有 $2^n-1$ 个节点。每个节点上有一个编号 $i$。根节点编号为 $1$,任意非叶子节点 $i$ 的左儿子的编号为 $i\times2$,右节点儿子的编号为 $i\times2+1$。每一个点有一个点权 $a_i$。
可是,ckj 把这棵树不小心弄丢了。但是他依然记得这棵树有一个特点:从编号为 $i$ 的叶子节点到树根每一个点的点权的 $\&$ 值 $\&$ 上 $i-2^{n-1}$ 为 $i-2^{n-1}$,并且 $0 \le a_i \le 2^{n - 1} - 1$。求满足要求这个树的点权的种数,对 $998244353$ 取模。
例如:
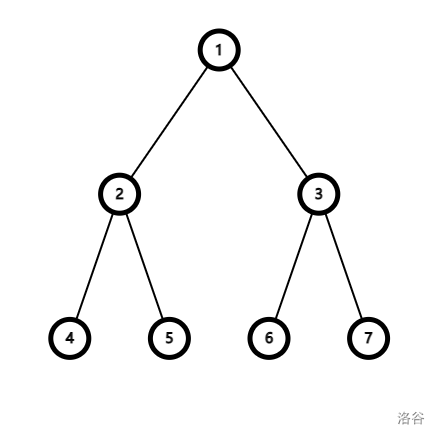
对于这棵满二叉树,需要满足以下要求:$a_1\&a_2\&a_4\&0=0,a_1\&a_2\&a_5\&1=1,a_1\&a_3\&a_6\&2=2,a_1\&a_3\&a_7\&3=3$。
输入格式
一行一个整数 $n$。
输出格式
一行一个整数,表示满足要求这个树的点权的种数对 $998244353$ 取模后的结果
说明/提示
**【样例 1 解释】**
可行的 $(a_1,a_2,a_3)$ 有 $(1,1,1)$ 和 $(1,0,1)$ 。
**【数据范围】**
| 测试点编号 | 分值 | 特殊性质 |
| :-: | :-: | :-: |
| $1$ | $5$ | $n=1$ |
| $2$ | $5$ | $n=2$ |
| $3$ | $5$ | $n=4$ |
| $4$ | $5$ | $n=7$ |
| $5$ | $5$ | $n=10$ |
| $6$ | $15$ | $n=100$ |
| $7$ | $15$ | $n=10^4$ |
| $8$ | $15$ | $n=10^8$ |
| $9$ | $15$ | $n=10^{16}$ |
| $10$ | $15$ | $n=10^{18}$ |
对于 $100\%$ 的数据,$1\le n\le 10^{18}$。