U226245 放书
题目描述
最近,约瑟夫买了很多书,准备把它们都放在书架上。他发现只有两种类型的书—— $A$ 型的高度为 $a$,厚度为 $1$ ,$B$ 型的高度为$b(a < b)$,厚度为$1$。每种类型的数量书本分别为 $n$ 和 $m$。而且他已经知道书架的高度是 $h(h \geq b)$。\
一开始,他把书架上的所有书都按高度从高到低排列,也就是说 $a$ 高度的书都在左边,$b$ 高度的书都在右边。这些书在书架上的总长度为 $n+m$。\
但是约瑟夫发现这些书上面还有一个空位,所以他准备从最右边开始选择 $k (0 \leq k \leq m - 1)$ 书将它们水平放置在其他书籍的顶部,以减少它们占用的长度。如果他以最佳方式排列这些书,他想知道最小宽度。
输入格式
输入的第一行给出了测试用例的数量 $T (1 \leq T \leq 10^3)$。 $T$ 测试用例如下。\
对于每个测试用例,只有一行包含五个整数 $a, b, n, m, h (1 \leq a < b \leq h \leq 10^6, 1 \leq n,m \leq 10^9)$
输出格式
对于每个测试用例,打印一行包含一个整数 $w$,表示最小宽度。
说明/提示
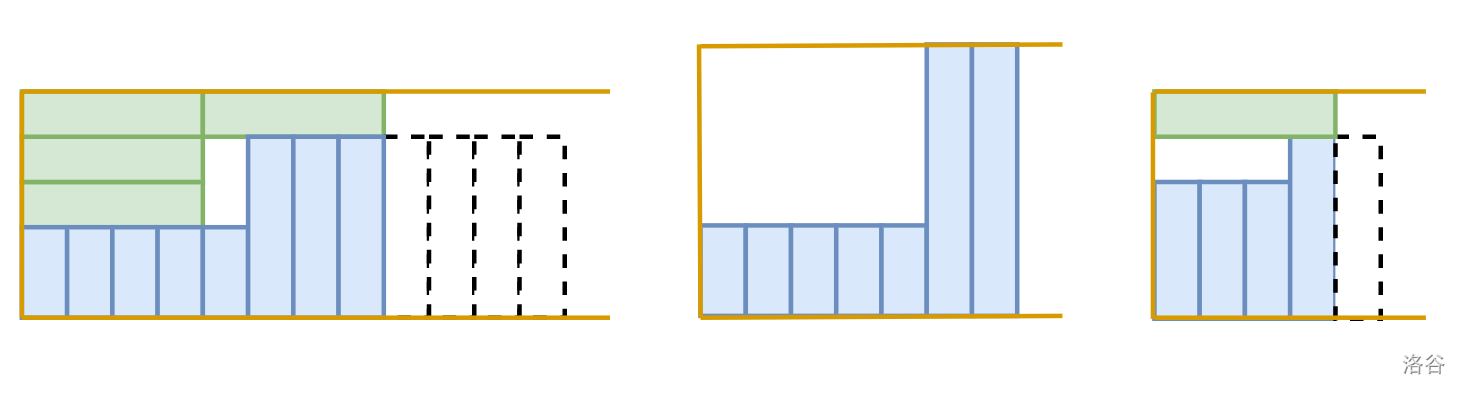
以下图片从左到右显示了测试用例 2、3 和 4 可能的书籍排列方式。