U228906 [NOIP 模拟赛] 树的搭建 (assemblage)
题目描述
Alice 和 Bob 要搭建一棵 $N$ 个点的树,点的标号为 $1\sim N$。他们现在已知树的形态,树上的每个节点有一个点权 $W_i$,但树上的边权尚未确定。现在 Alice 和 Bob 有 $N-1$ 个正整数 $A_i$。他们需要把这些正整数,分配给树的 $N-1$ 条边(每个正整数恰好作为一条边的边权),作为每条边的边权,来完成这棵树的搭建。
定义 $F_{u,v}$ 表示 $u,v$ 简单路径上的最小边权。定义二人搭建一棵树的代价为:
$$\sum\limits_{u=1}^N\sum\limits_{v=u+1}^NW_u\times W_v\times F_{u,v}$$
请你帮助 Alice 和 Bob 计算出搭建这棵树所需要的最小代价。
输入格式
第一行一个正整数 $N$。
第二行 $N$ 个正整数,第 $i$ 个正整数 $W_i$ 表示 $i$ 号点的点权。
接下来 $N-1$ 行,每行两个正整数 $x_i,y_i$,表示一条连接 $x_i,y_i$ 的边。
最后一行 $N-1$ 个正整数 $A_i$,表示待分配的 $N-1$ 个边权值。
输出格式
一行一个正整数,表示答案。
说明/提示
【输入输出样例 $1$】
见选手目录下的 $assemblage/assemblage1.in$ 和 $assemblage/assemblage1.ans$。
【样例 $1$ 解释】
最优的两种分配边权的方案如下:

【输入输出样例 $2$】
见选手目录下的 $assemblage/assemblage2.in$ 和 $assemblage/assemblage2.ans$。
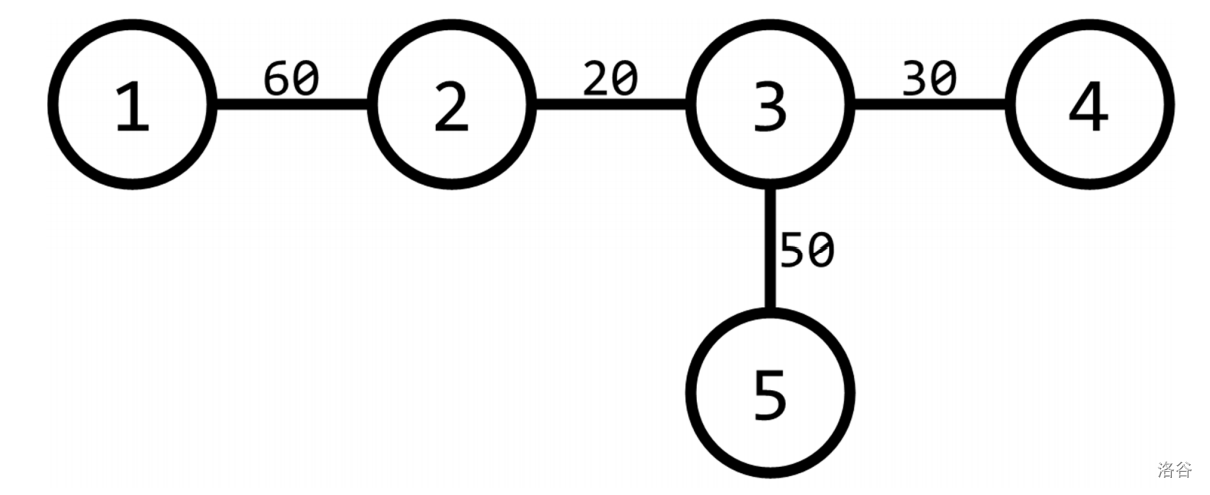
【样例 $2$ 解释】
唯一一种最优的分配边权的方案如下:
【输入输出样例 $3$】
见选手目录下的 $assemblage/assemblage3.in$ 和 $assemblage/assemblage3.ans$。
【输入输出样例 $4$】
见选手目录下的 $assemblage/assemblage4.in$ 和 $assemblage/assemblage4.ans$。
【输入输出样例 $5$】
见选手目录下的 $assemblage/assemblage5.in$ 和 $assemblage/assemblage5.ans$。
【数据范围与约定】
| 测试点编号 | $N=$ | 特殊性质 |
| :----------: | :----------: | :----------: |
| $1$ | $2$ | 无 |
| $2\sim3$ | $3$ | 无 |
| $4\sim5$ | $8$ | 无 |
| $6\sim7$ | $10$ | 无 |
| $8\sim10$ | $18$ | 所有 $x_i=1$ |
| $11\sim13$ | $18$ | 无 |
| $14\sim15$ | $21$ | 无 |
| $16\sim17$ | $22$ | 无 |
| $18\sim20$ | $23$ | 无 |
对于全部数据,$2\le N\le23,1\le a_i