U246726 「KDOI-01」清平乐
题目背景
优美的乐曲,楚楚动人,令人陶醉……
题目描述
一天, $\texttt{Reg}$ 心血来潮,想编一首美妙的乐曲。他想出了很多旋律的片段,就差把他们组合到一起了!
不过, $\texttt{Reg}$ 并没有多少音乐天赋,所以,有些片段很优美,有些就呕哑嘲哳难为听(?)。我们可以把每段音乐的动听程度抽象为一个数 $w_i$,一段乐曲的动听程度为其中的所有**互不相同**音乐片段动听程度的和。动听程度是 $\texttt{Reg}$ 自己定的,所以 $\texttt{Reg}$ 会频繁地修改它们。
在这些音乐片段中,还有一些非常特殊的片段:开头和结尾。结尾是不能接在任何乐段前面的乐段(编号为 $1$),开头则为不能接在任何乐段后面的乐段。因为 $\texttt{Reg}$ 太菜了,所以 $\texttt{Reg}$ 想出的每段音乐只能接在一个乐段前面(除结尾),并且任意乐段不能编成循环。
现在, $\texttt{Reg}$ 想出了一大堆的片段与一个结尾。$\texttt{Reg}$ 觉得一个乐段太单薄了,他决定用两种方式演奏这些乐段:
1. 用编号为 $x,y$ 的乐段开头。设接 $x,y$ 乐段后方最近的共同乐段为 $T$,则演奏到 $T$ 后**立刻停止**。该方式也被称为“高低声部演奏”。
如图所示,演奏部分已被红圈框出:
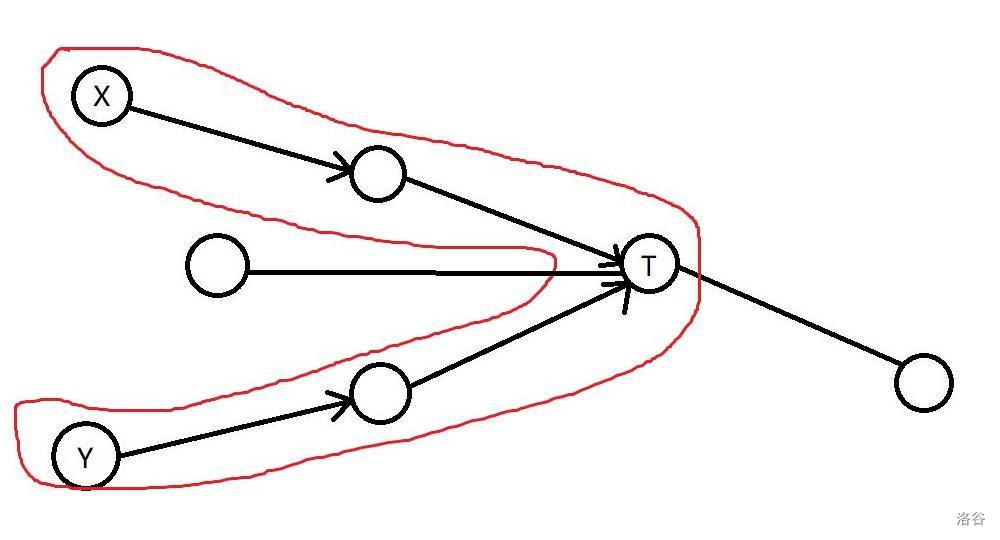
2. 用编号为 $T$ 的乐段作为结尾,从所有在它之前的开头同时演奏,直到乐段 $T$。该方式也被称为“多声部演奏”。
如图所示:
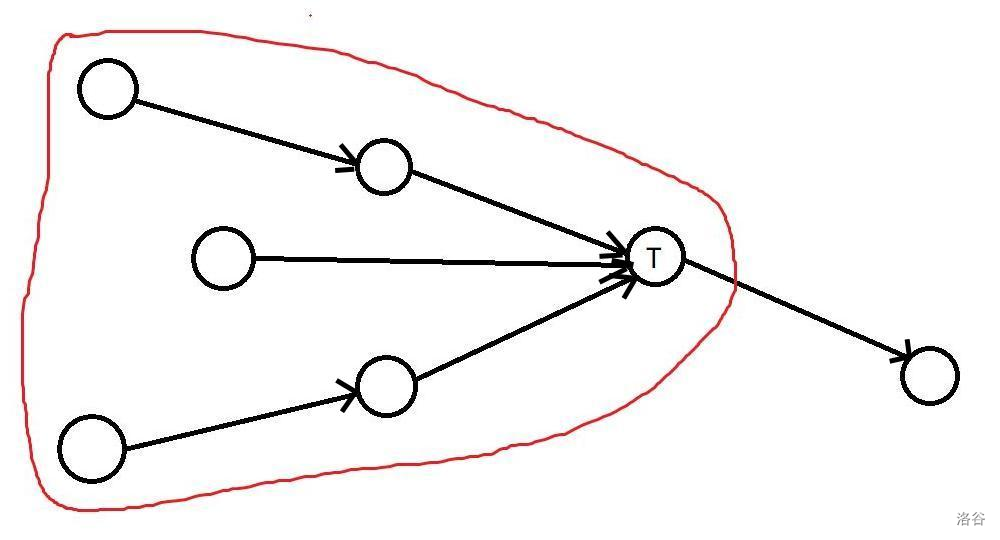
$\texttt{Reg}$ 一直都在思考,所以他会想出一个新的尾声,并接在原来的结尾上,取代原来的结尾(即原来所有音乐片段的编号 $+1$,该片段编号为 $1$)。现在,给出这些音乐片段及他们的相连关系, $\texttt{Reg}$ 想让你帮他求出一段乐曲的动听程度。
输入格式
第一行两个整数 $n,q$ 表示音乐片段数与操作数。
下一行有 $n$ 个正整数,表示每个片段的动听程度。
接下来 $n-1$ 行,每行两个数 $u,v$,代表编号为 $u$ 的片段之间可以接在编号为 $v$ 的乐段后面。
之后 $q$ 行,每行一个操作:
- `1 x y`:求以 $x,y$ 做高低声部开头时乐曲的动听程度。
- `2 T`:求解以 $T$ 做结尾的多声部乐曲的动听程度。
- `3 x w`:将编号为 $x$ 的片段动听程度加上 $w$。
- `4 w`:加入一个动听程度为 $w$ 的尾声。
输出格式
对于 `1`,`2` 操作,输出答案。
说明/提示
样例解释:
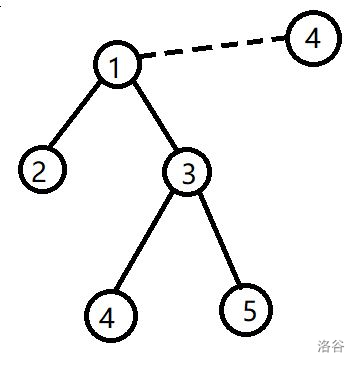
其中,$2,4,5$ 为开头, $1$ 为结尾。在 $4$ 操作后,结尾被新节点代替。
| 测试点编号 | 数据范围 | 特殊性质 |
| :-----------: | :-----------: | :-----------: |
| $1\sim4$ | $n,q\le100$ | 特殊性质 A |
| $5\sim10$ | $n,q\le10^6$ | 特殊性质 A |
| $13\sim18$ | $n,q\le10^6$ | 特殊性质 B |
| $11,12,19,20$ | $n,q\le10^6$ | 无 |
特殊性质 A:数据不包含操作 `4`。
特殊性质 B:数据保证每段音乐最多只能接在另一段后面。
本题IO量巨大,请使用较快的读入方式。这里给出快读模板:
```cpp
inline void read(int &x) {
x=0;
register int f=1;
register char c=getchar();
while(c'9') {
if(c=='-') f=-1;
c=getchar();
}
while (c>='0'&&c