U248852 tREe

曾用于校内训练：[YAOI Round #26 (Div.1+Div.2) F. 猴皮面包树](http://47.110.12.131/problem/5288) ofbwyx 正站在一个根为 $r$ 的树上。ofbwyx 希望了解关于树的一些信息。 不过，ofbwyx 只知道两个点之间是否直接有边相连，但不知道哪个点是另一个的祖先。

第一行三个正整数 $n,r,q$，分别表示树的节点个数，树根编号和询问个数。 接下来 $n-1$ 行每行两个正整数 $u,v$ 表示 $u,v$ 之间有边相连。 接下来 $q$ 行每行两个正整数 $op,x$，若 $op=1$ 则询问 $x$ 的父节点编号，$op=2$ 则询问 $x$ 的深度，若 $op=3$ 则询问离 $x$ 最远的节点的距离（令每条边的长度均为 $1$），若 $op=4$ 则询问此节点的子树大小。

第一行三个正整数 $n,r,q$，分别表示树的节点个数，树根编号和询问个数。 接下来 $n-1$ 行每行两个正整数 $u,v$ 表示 $u,v$ 之间有边相连。 接下来 $q$ 行每行两个正整数 $op,x$，若 $op=1$ 则询问 $x$ 的父节点编号，$op=2$ 则询问 $x$ 的深度，若 $op=3$ 则询问离 $x$ 最远的节点的距离（令每条边的长度均为 $1$），若 $op=4$ 则询问此节点的子树大小。

输出 $q$ 行，每行一个答案回答询问。

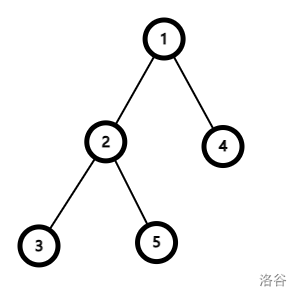
**样例解释**  数据输入了一个形如上图的树，在树中：节点 $3$ 的父节点为 $2$；节点 $2,3$ 的深度分别为 $2,3$；离节点 $5$ 距离最远的是节点 $4$，距离为 $3$；离节点 $2$ 距离最远的是节点 $4$，距离为 $2$；节点 $2$ 的子树有 $2,3,5$ 三个点，大小为 $3$；节点 $1$ 的子树有 $1,2,3,4,5$ 五个点，大小为 $5$。 样例中的空行只是用于分隔连边和询问两个部分的，实际数据中并无这个空行，不过空行也并不影响读入。 ------------ **数据范围** ------------ **数据范围** | 测试点编号 | $n,q\le$ | 特殊性质 | | :--------: | :-------------: | :-----------------------: | | 1 | $100$ | $op$ 只会等于 $1$ 或 $2$ | | 2 | $100$ | $op$ 只会等于 $3$ | | 3 | $100$ | $op$ 不等于 $4$ | | 4~5 | $10^4$ | $op=3$ 的数量不大于 $100$ | | 6~10 | $8 \times 10^5$ | 无 | 对于 $100\%$ 的数据，保证 $1 \le u_i,v_i,r \le n,q \le 10^6$，保证数据随机且构成一棵树。 ------------ **提示** 本题 4~10 测试点输入量较大，为了使输入不影响做题，现给出快速输入输出，请选手酌情使用。 ```cpp int read(){ int w=0,ch=getchar(); while(ch'9')ch=getchar(); while(ch>='0'&&ch9)write(x/10); putchar(x%10+48); } ``` 用法示例：`a=read()`：读入一个非负整数 `a`；`write(a)`：输出一个非负整数 `a`。