U277325 Larry Jr.

【Larry Jr.个体】是独立游戏《The Binding of Isaac》中的 Boss 关怪物之一。 【Larry Jr.个体】长得像一条贪吃蛇，由 $n$ 节身体构成。假设你仅能从其左端或右端攻击。当你从左端攻击一次，将消灭其最左端的一节身体；当你从右端攻击一次，将消灭其最右端的一节身体。当某条【Larry Jr.个体】剩余的身体节数为 $0$，称其被击败。 记某条【Larry Jr.个体】编号为 $i$ 的身体节为：在该个体的任何身体节都未被消灭时，从左向右数的第 $i$ 个身体节。 在战斗开始前，给定两个 $[1,n-1]$ 间的整数 $l,r(l\lt r)$，你有一次机会任意选择一个 $[l,r]$ 间的整数，记为 $x$，并将整条【Larry Jr.个体】分成两段： - 编号为 $[1,x]$ 的身体节为第一段，记为 $L_1$ - 编号为 $[x+1,n]$ 的身体节为第二段，记为 $L_2$ 以下 $L_1,L_2$ 将**分别作为独立的【Larry Jr.个体】**。 定义击败某条有 $n$ 节身体的【Larry Jr.个体】的方案为：一个包含 $n$ 个整数的排列，排列的第 $i$ 项表示第 $i$ 次攻击所消灭身体节的编号。 对于两种方案（分别记作 $a,b$），若存在 $i$，使得 $a_i\ne b_i$，则称这两种方案不同。 记击败 $L_1$ 的不同方案数为 $k_1$，击败 $L_2$ 的不同方案数为 $k_2$。 你需要求出： - 在所有可能的 $x$ 中，使得 $(k_1+k_2)$ 最小的 $x$ 值，以及此时的 $(k_1+k_2) \mod 998244353$ 的值。如果 $x$ 有多种可能取值，输出最小的 $x$。 - 在所有可能的 $x$ 中，使得 $(k_1+k_2)$ 最大的 $x$ 值，以及此时的 $(k_1+k_2) \mod 998244353$ 的值。如果 $x$ 有多种可能取值，输出最小的 $x$。

#### 本题每个测试点有多组数据 每个测试点第一行，一个整数 $T$，代表数据组数。 每组数据包含三个整数 $n,l,r$。

共 $T$ 行，每行四个整数。依次为： - 使 $(k_1+k_2)$ 最小的 $x$ 值，此时的 $(k_1+k_2) \mod 998244353$ 值； - 使 $(k_1+k_2)$ 最大的 $x$ 值，此时的 $(k_1+k_2) \mod 998244353$ 值。

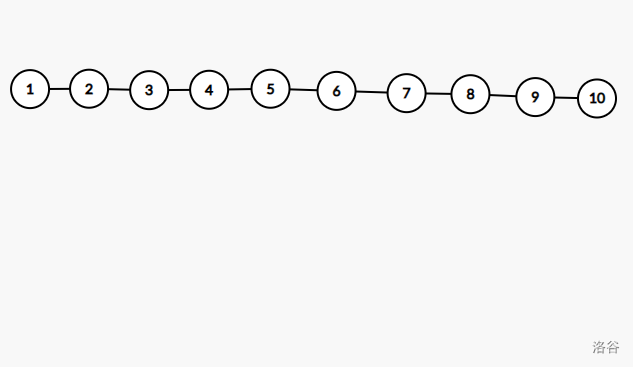
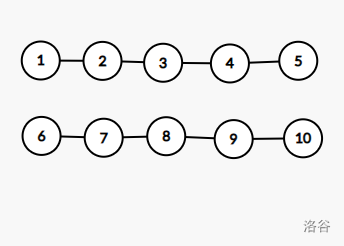
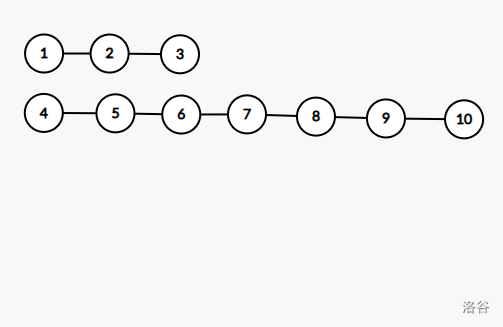
#### 样例解释 #1 对于本样例第一组数据的切割方案，作图解如下： 切割前的形状：  最小的切割方案：  最大的切割方案：  #### 数据范围 对于 $20\%$ 的数据，$n\le30$ 对于 $50\%$ 的数据，$n\le10^5,T\le100$ 对于 $100\%$ 的数据，$1\le l\lt r\lt n\le10^{18},1\le T\le10^5$