U280360 天空度假山庄

注意本题和课件里的题目《天空度假山庄》略有不同。本题中 $f(G)$ 的定义为连通块个数**的平方**的期望值（虽然总体差别不大233

云浅与 Yoimiya 一起来到了「天空度假山庄」。「天空度假山庄」中有一个 $n$ 点 $m$ 边的无向图 $G$，图中点的编号分别为 $1,2,\cdots,n$，边的编号分别为 $1,2,\cdots,m$。 度假山庄已经很久没有打扫了，因此图中的边已经模糊不清。具体来说： - 第 $i$ 条边连接的两个端点分别为 $u_i$ 和 $v_i$。 - 这条边上落下了许多灰尘，有 $p_i$ 的概率直接消失。这里保证 $0

第一行两个正整数 $n,m$。 接下来 $m$ 行，第 $i+1$ 行有 $4$ 个正整数 $u_i,v_i,x_i,y_i$，表示一条边。其中： - $u_i,v_i$ 表示这条边的两个端点。 - 这条边消失的概率即为 $p_i=\frac{x_i}{x_i+y_i}$。

输出 $n$ 行，第 $i$ 行有 $n-i+1$ 个整数，表示 $f(G[i:i]),f(G[i:i+1]),\cdots,f(G[i:n])$ 的值。

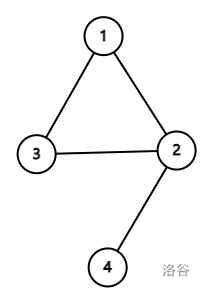
样例中，图的形态为：  以 $f(G[1:n])$ 为例： 例如，当边 $(1,2),(2,3)$ 消失，$(1,3),(2,4)$ 存在时，图中连通块个数为 $2$。这种情况发生的概率是 $\frac{1}{2}\times \frac{1}{3}\times \frac{3}{4}\times\frac{3}{5}=\frac{3}{40}$。 不难验证，连通块个数为 $1,2,3,4$ 的概率分别为 $\frac{17}{40},\frac{13}{30},\frac{1}{8},\frac{1}{60}$，因此连通块个数的平方的期望值为 $$ f(G[1:n])=\frac{17}{40}\times 1^2+\frac{13}{30}\times 2^2+\frac{1}{8}\times 3^2+\frac{1}{60}\times 4^2=\frac{71}{20} $$ 在 $\bmod 998244353$ 意义下为 $648858833$，因此你应该在第一行的第 $4$ 列输出 $648858833$。 ### 测试点约束 对于 $100\%$ 的数据，$2\le n\le 19,1\le m\le \frac{n(n-1)}{2},1\le x_i,y_i