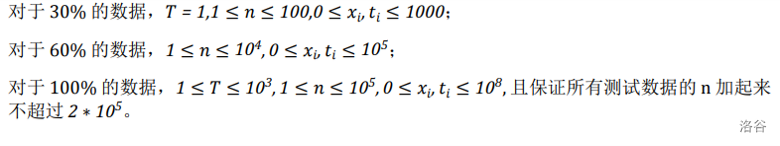U284661 [CSP-J2022 山东补测]【官方数据】宴会（banquet）

[CF1730B 原题。](https://www.luogu.com.cn/problem/CF1730B) 今人不见古时月，今月曾经照古人。梦回长安，大唐风华，十里长安花，一日看尽。 唐长安城是当时世界上规模最大、建筑最宏伟、规划布局最为规范化的一座都城。其营建制度规划布局的特点是规模空前、创设皇城、三城层环、六坡利用、布局对称、街衢宽阔、坊里齐整、形制划一、渠水纵横、绿荫蔽城、郊环祀坛。而所谓的十里长安街，位于长安城的中轴线上，即唐长安城的朱雀大街，又称承天门大街。唐朝官员们住在各个“坊”里，上朝下朝都需要通过朱雀大街。 为了保持各大家族的联系和友谊，各官员往往会每月办一次宴会。为了方便描述，我们把朱雀大街看成一个数轴，各官员所居住的“坊”缩略为数轴上的一个坐标点。大家决定选一处地点（该地点是数轴上的某一个点，不一定坐标点）办宴会。由于唐朝宵禁严格，大家又都希望交流时间尽可能长，因此想要使宴会开始时间尽可能早。又因为大唐注重礼仪，因此，参加宴会的官员会花一定时间盛装打扮过后才前往宴会地点（不一定是坐标点）。

更具体地，一条纵向的街道上（相当于一维坐标）有 $n$ 个人居住，其中第 $i$ 个人居住在 $x_i$（非负整数）位置（坐标点）上。每月他们会选择在 $x_0$（数轴上的某一个点，不一定坐标点）处举办宴会。 已知第 $i$ 个人从 $x_i$ 出发前往宴会地点 $x_0$ 处需要花费 $|x_i-x_0|$ 的时间，另外，他还需要花费 $t_i$ 的时间进行打扮，换言之，他共需要花费 $|x_i-x_0|+t_i$ 的时间到达宴会举办处。 假设**初始时刻为 $\mathbf 0$**。这 n 个人开始打扮和出发前往宴会处，他们想要使得宴会的开始时间尽可能早，于是向你求助，请你帮助他们确定好最优的宴会举办地点 $x_0$。 注：$|x_i-x_0|$ 表示 $x_i$ 与 $x_0$ 之差的绝对值，且题目中 n 个人的居住地点坐标均为整数。

第一行一个正整数 $T$，表示测试数据的组数。 接下来对于每组测试数据（注意：每组测试数据有 $3$ 行数据，以下共 $3 \times T$ 行数据）： 第一行一个正整数 $n$，表示总官员人数。 第二行共 $n$ 个非负整数 $x_1,x_2,...,x_n$ 分别表示这 $n$ 个人在数轴上的坐标。 第三行共 $n$ 个非负整数 $t_1,t_2,...,t_n$ 分别表示这 $n$ 个人出发前的打扮时间。

共输出 $T$ 行数据，对于每组测试数据，输出一行一个**实数**（如果是整数按整数输出，如果有小数，保留 $1$ 位小数输出），表示使宴会开始时间最早的最优举办地点坐标 $x_0$。（很显然，$x_0$ 都是唯一的）

### 样例解释 初始时刻为 $0$。 对于第一组测试数据只有 $1$ 个人，坐标为 $0$，打扮时间为 $3$，很显然 $x_0$ 就定在坐标 $0$ 处，使得宴会开始时间为 $3$ 且最早。 对于第二组测试数据有 $2$ 个人，坐标分别为 $3$、$1$，打扮时间均为 $0$，很显然 $x_0$ 定在坐标 $2$ 处，使得宴会开始时间为 $1$ 且最早。 对于第三组测试数据有 $2$ 个人，坐标分别为 $1$、$4$，打扮时间均为 $0$，很显然 $x_0$ 定在坐标 $2.5$ 处，使得宴会开始时间为 $1.5$ 且最早。 ### 数据规模与约定