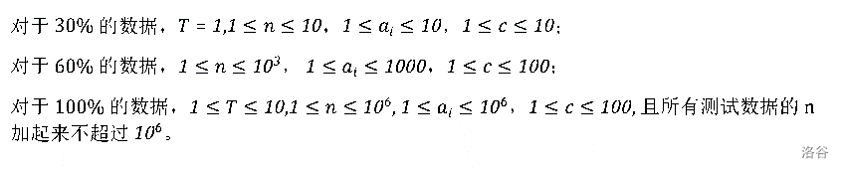U284673 [CSP-X2022 山东补测]【官方数据】摧毁(destroy)
题目描述
>坐地日行八万里,巡天遥看一千河。
2077 年,人类不仅仅是赛博科技得到了发展,太空技术也已经得到了极大的发展。地球的不同外轨道上已经充斥着各种功能用途的人造卫星。因为一个轨道上的卫星数量是有上限的,且卫星更新换代速度很快,如果想要发射新的卫星,需要把所有旧的卫星摧毁。
人类有两种不同的武器可以摧毁卫星,具体如下(其中 $PW$ 为新的能量单位):
1. 使用定点激光武器花费 $1 PW$ 的代价摧毁任意轨道上指定的一个卫星。
2. 使用脉冲轨道武器花费 $c PW$ 的代价把某一轨道上的所有卫星摧毁。
现在有 $n$ 个旧卫星分布在不同的外轨道上,你的任务是摧毁这些旧卫星。给出这 $n$ 个卫星的轨道编号,求将这些卫星全部摧毁的最小代价是多少?
输入格式
第一行一个正整数 $T$,表示测试数据组数。
接下来对于每组测试数据(注意:每组测试数据有 $2$ 行数据,以下共 $2 \times T$ 行数据):
第一行两个正整数 $n$ 和 $c$ 表示需要摧毁的卫星数量和使用脉冲轨道武器的代价。
第二行是 $x_1,x_2,...,x_n$,其中 $x_i$ 表示第 $i$ 个卫星的轨道编号。
输出格式
输出 $T$ 行答案,对于每组测试数据,输出一行一个整数表示摧毁所有卫星的代价。
说明/提示
### 样例说明:
对于第一组测试数据,使用脉冲武器的代价为 $1 PW$。轨道 $1$ 上有 $2$ 个卫星,轨道 $2$ 上有 $3$ 个卫星,轨道 $4$ 上有 $2$ 个卫星,轨道 $5$ 上有 $3$ 个卫星。因此对于轨道 $1,2,4,5$,均使用脉冲武器各花费 $1PW$ 的代价可全部摧毁,总的代价为 $4 PW$,很显然该方案为总代价最小方案。
对于第二组测试数据,使用脉冲武器的代价为 $2 PW$。轨道 $1$ 上有 $1$ 个卫星,轨道 $2$ 上有 $3$ 个卫星,轨道 $3$ 上有 $1$ 个卫星。因此,对于轨道 $1$ 采用激光武器,轨道 $2$ 采用脉冲武器,轨道 $3$ 采用激光武器可全部摧毁所有卫星,总的代价为 $4 PW$,很显然该方案使得总代价最小。
### 数据范围