U310721 Points

数轴上存在 $n$ 个点，第 $i$ 个点的坐标为 $x_i$，点权为 $w_i$。 点可以被连接，将点 $i$ 和点 $j$ 连接的代价为 $(x_i-x_j)^2+w_i+w_j$，每个点至多被连接两次，一个连接不能覆盖其他连接。 连接具有传递性，也就是说，若点 $a$ 与 $b$ 连接，$b$ 与 $c$ 连接，那么 $a$ 与 $b$ 连接。 你需要求出欲使点 $1$ 与点 $n$ 连接所需的最小代价。

第一行一个正整数 $n$。 接下来 $n$ 行，第 $i$ 行两个整数 $x_i,w_i$，分别表示第 $i$ 个点的坐标和点权。

输出使点 $1$ 与点 $n$ 连接的最小代价。

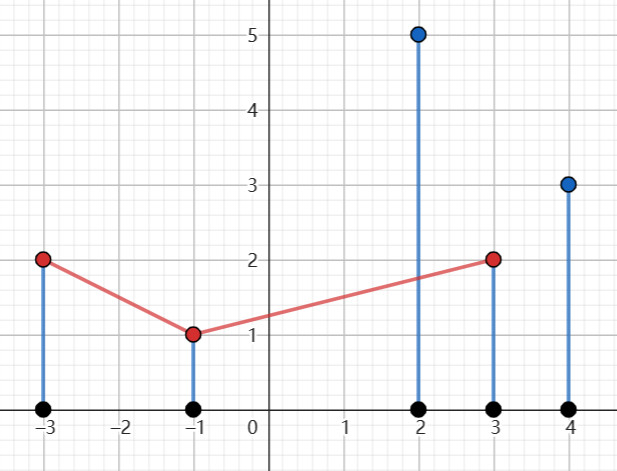
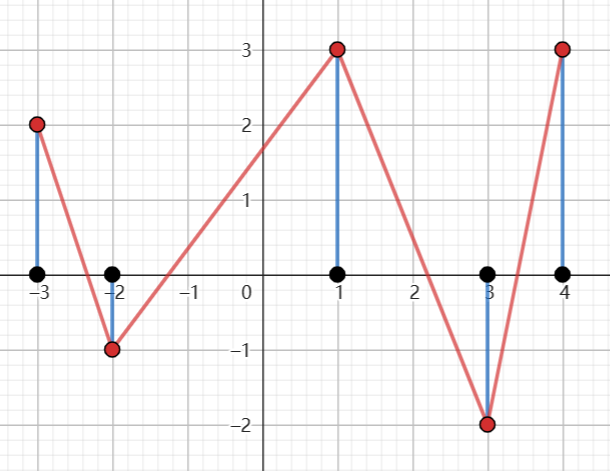
### 样例解释   ### 数据范围 |测试点编号|$n\le$|$\max \vert x_i\vert\le$|$\max \vert w_i\vert\le$|特殊性质|分值| |:--:|:---:|:-:|:-:|:--:|:-:| |$1$|$12$|$10$|$10$|无|$10$| |$2\sim4$|$1\times 10^4$|$1\times 10^4$|$1\times 10^4$|无|$20$| |$5\sim 8$|$2\times 10^5$|$1\times 10^7$|$1\times 10^7$|无|$40$| |$9\sim 10$|$5\times 10^6$|$1\times 10^7$|$1\times 10^7$|$A$|$30$| $A$：$x_i$ 严格单调递增。 对于 $100\%$ 的数据，$1\le n\le 5\times 10^6,|x_i|,|w_i|\le 10^7$。 ### 注意 **本题最大读入量约 80MB，请使用较快的输入输出方式，请注意常数因子对程序运行时间的影响**。 保证答案在 64 位有符号整数范围内。 [题解](https://www.cnblogs.com/TKXZ133/p/17532085.html)