U372841 最小生成树

> ​ 树是大自然最富有创意的艺术家。 ​ Capps 很喜欢树，可是 Capps 不会最小生成树问题，这是一道最小生成树问题，请你帮帮 Capps 。 ​ 给出一个 $n$ 个点的图，点编号从 $1$ 到 $n$ ， $i$ 号点的点权为 $a_i$ 。对于 $\forall i,j$ $(1\le i\lt j\le n)$ $i$ 号点 和 $j$ 号点之间存在一条无向边，边权为 $a_i+a_j$ 。请求出这个无向图的**最小生成树的边权和**。 ​ 请回忆： - 在 $n$ 个点的图 $G$ 中选择 $n-1$ 条边，这 $n-1$ 条边和 $n$ 个点构成图 $H$ ，图 $H$ 满足其中任意两个点之间都存在一条路径使得这两个点联通，那么图 $H$ 是图 $G$ 的一个**生成树**。 - 在图 $G$ 的所有生成树中，边权和最小的生成树称为图 $G$ 的**最小生成树**。

本题有多个样例，第一行一个样例数 $T$ $(1\le T \le 5\times 10^3)$。 对于每个样例： 第一行一个整数 $n$ $(1\le n \le 5\times 10^3)$，表示图的点数。 第二行 $n$ 个整数，第 $i$ 个整数表示 $a_i$ $(1\le a_i\le 3\times 10^5)$，即 $i$ 号点的点权。 对于所有样例，保证 $\sum n \le 5 \times 10^3$。

对于每个样例输出一行一个整数表示询问的图的最小生成树的边权和，共输出 $T$ 行。

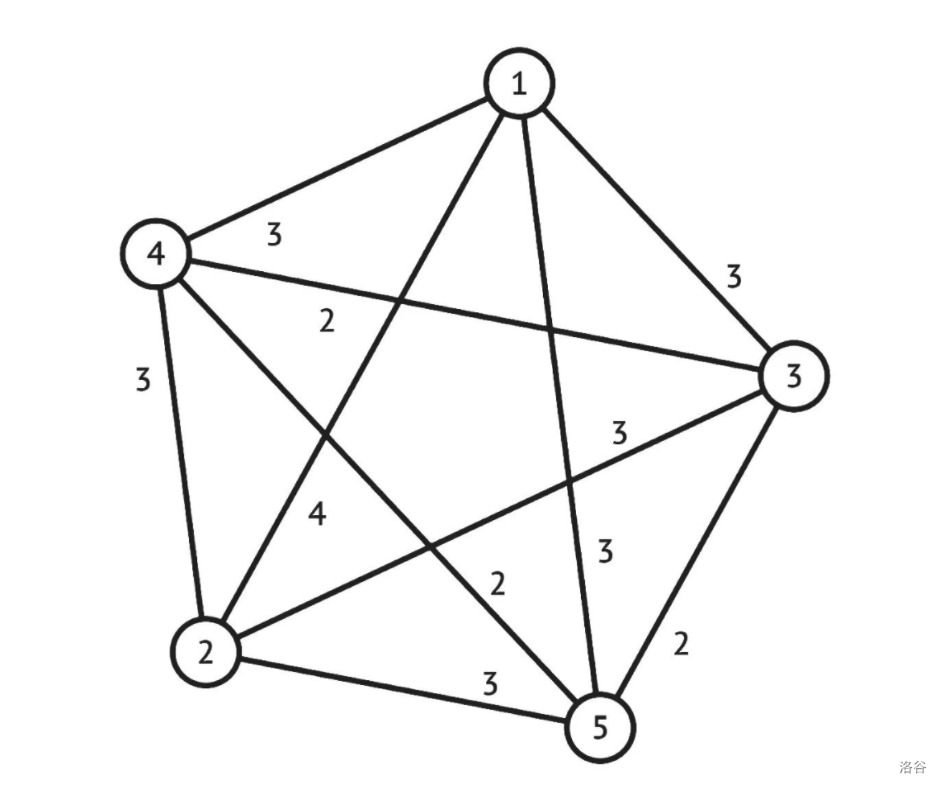
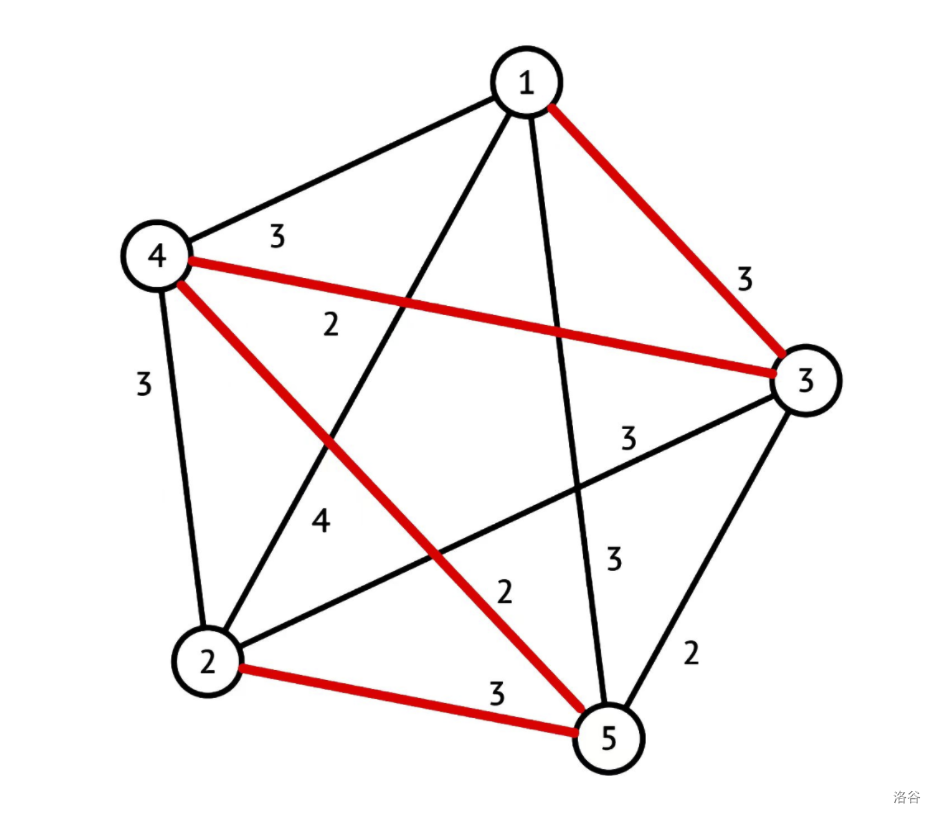
样例1中的图为 :  其中一个最小生成树可以是: